题目内容
（2012•大连模拟）设集合A={（x，y）||x|+|y|≤2}，B={（x，y）∈A|y≤x2}，从集合A中随机地取出一个元素P（x，y），则P（x，y）∈B的概率是（ ）
分析：集合A是一个正方形区域的内部及边界，4个顶点是（0，2）（0，-2）（2，0）（-2，0），集合B是抛物线y=x2 下方的区域，分别求出面积，即可求出P（x，y）∈B的概率．
解答：解：集合A是一个正方形区域的内部及边界，4个顶点是（0，2）（0，-2）（2，0）（-2，0），集合B是抛物线y=x2 下方的区域
由
，可求得两图象在第一象限的交点坐标为（1，1）
∵抛物线y=x2 下方的区域的面积，根据对称性，可得面积为4+ 2
x2dx+2×
×1×1=5+2×
x3
=
，
正方形的面积为
=8，
∴P（x，y）∈B的概率是
=
故选B．
由
|
∵抛物线y=x2 下方的区域的面积，根据对称性，可得面积为4+ 2
| ∫ | 1 0 |
| 1 |
| 2 |
| 1 |
| 3 |
| | | 1 0 |
| 17 |
| 3 |
正方形的面积为
| 4×4 |
| 2 |
∴P（x，y）∈B的概率是
| ||
| 8 |
| 17 |
| 24 |
故选B．
点评：本题考查几何概型，考查学生分析解决问题的能力，其中确定抛物线y=x2 下方的区域的面积是关键．
练习册系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
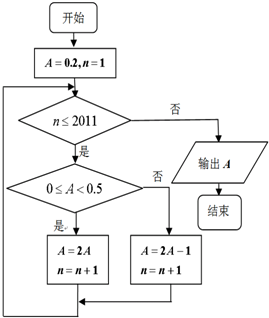（2012•大连模拟）已知某程序框图如图所示，则该程序运行后，输出的结果为（ ）