题目内容
(2012•大连模拟)若(
-
)n展开式中二项式系数之和是1024,常数项为45,则实数a的值是
| x |
| a |
| x2 |
±1
±1
.分析:根据题意,由二项式系数的性质可得2n=1024,解可得n=10,进而可得则(
-
)n展开式的通项,令x的指数为0,可得r的值为2,即(
-
)n展开式中的常数项为T3,求出T3,结合题意有a2•C102=45,解可得答案.
| x |
| a |
| x2 |
| x |
| a |
| x2 |
解答:解:根据题意,(
-
)n展开式中二项式系数之和是1024,有2n=1024,则n=10,
则(
-
)n展开式的通项为Tr+1=C10r•(
)10-r•(-
)r=(-1)r•ar•C10r•x
,
令
=0,可得r=2,
则(
-
)n展开式中的常数项为T3=a2•C102,
则有a2•C102=45,即a2=1,
则a=±1,
故答案为±1.
| x |
| a |
| x2 |
则(
| x |
| a |
| x2 |
| x |
| a |
| x2 |
| 10-5r |
| 2 |
令
| 10-5r |
| 2 |
则(
| x |
| a |
| x2 |
则有a2•C102=45,即a2=1,
则a=±1,
故答案为±1.
点评:本题考查二项式定理的应用,解题的关键是由二项式系数的性质求出n,并得到该二项式的通项.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
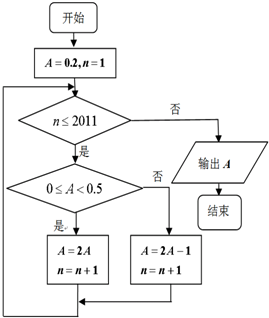 (2012•大连模拟)已知某程序框图如图所示,则该程序运行后,输出的结果为( )
(2012•大连模拟)已知某程序框图如图所示,则该程序运行后,输出的结果为( )