题目内容
已知曲线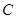 的极坐标方程是ρ=2,以极点为原点,极轴为
的极坐标方程是ρ=2,以极点为原点,极轴为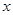 轴的正半轴建立平面直角坐标系
轴的正半轴建立平面直角坐标系
(1) 写出曲线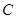 的直角坐标方程;
的直角坐标方程;
(2)若把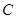 上各点的坐标经过伸缩变换
上各点的坐标经过伸缩变换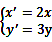 后得到曲线
后得到曲线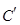 ,求曲线
,求曲线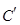 上任意一点到两坐标轴距离之积的最大值.
上任意一点到两坐标轴距离之积的最大值.
【答案】
⑴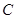 的普通方程为 x2+y2=4 ;⑵最大值为12.
的普通方程为 x2+y2=4 ;⑵最大值为12.
【解析】(1)根据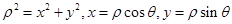 进行转化即可。
进行转化即可。
(2)根据条件可求出伸缩变换后的方程为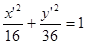 ,然后根据
,然后根据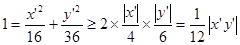 ,即可求出
,即可求出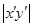 ≤12.要注意取等的条件。
≤12.要注意取等的条件。
解:.⑴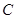 的普通方程为 x2+y2=4 (4分)
的普通方程为 x2+y2=4 (4分)
⑵(方法一)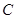 经过伸缩变换{
经过伸缩变换{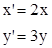 后,
后,
{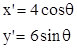 (
(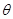 为参数),(7分)
为参数),(7分)
∴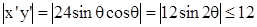 当
当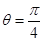 时,取得“=”.
时,取得“=”.
∴曲线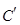 上任意一点到两坐标轴距离之积的最大值为12.
(10分)
上任意一点到两坐标轴距离之积的最大值为12.
(10分)
(方法二) 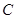 经过伸缩变换{
经过伸缩变换{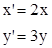 后{
后{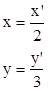 ,
,
∴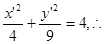 C’:
C’: 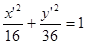 (7分)
(7分)
∵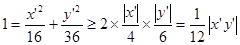 ,∴
,∴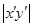 ≤12.
≤12.
当且仅当 时,取“=”.
时,取“=”.
∴曲线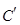 上任意一点到两坐标轴距离之积的最大值为12. (10分)
上任意一点到两坐标轴距离之积的最大值为12. (10分)

练习册系列答案
相关题目
已知曲线的极坐标方程为ρ=4cos2
-2,则其直角坐标下的方程是( )
| θ |
| 2 |
| A、x2+(y+1)2=1 |
| B、(x+1)2+y2=1 |
| C、(x-1)2+y2=1 |
| D、x2+(y-1)2=1 |
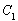
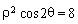
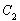
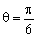
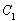
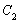
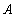
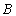
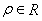
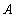
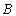
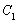

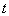
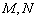
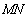
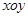 的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同,已知曲线
的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同,已知曲线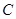 的极坐标方程为
的极坐标方程为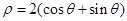 .
.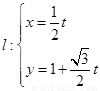 (
(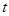 为参数)与曲线C交于
为参数)与曲线C交于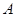 ,
,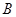 两点,与
两点,与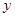 轴交于
轴交于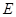 ,求
,求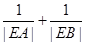 的值.
的值. 的极坐标方程是
的极坐标方程是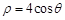 ,以极点为原点,极轴为
,以极点为原点,极轴为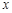 轴正方向建立平面直角坐标系,直线的参数方程是:
轴正方向建立平面直角坐标系,直线的参数方程是: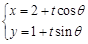 (为参数).
(为参数).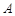 ,
,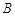 两点,点
两点,点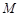 的直角坐标为
的直角坐标为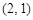 ,若
,若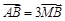 ,求直线的普通方程.
,求直线的普通方程.