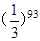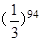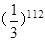题目内容
观察下列各式: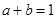 ,
,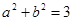 ,
,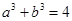 ,
,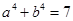 ,
,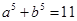 ,
, 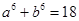 ,则
,则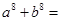 ( )
( )
A.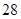 | B.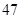 | C.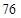 | D. |
B.
解析试题分析:观察可得各式的值构成数列1,3,4,7,11, ,其规律为从第三项起,每项等于其前相邻两项的和,所求值为数列中的第八项.继续写出此数列为1,3,4,7,11,18,29,47,76,123, ,第十项为47,即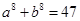 .
.
考点:归纳推理.

练习册系列答案
相关题目
用反证法证明命题“三角形的内角至多有一个钝角”时,假设正确的是( )
| A.假设至少有一个钝角 | B.假设至少有两个钝角 |
| C.假设没有一个钝角 | D.假设没有一个钝角或至少有两个钝角 |
用火柴棒摆“金鱼”,如图所示: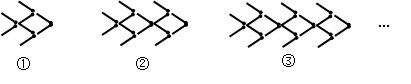
按照上面的规律,第4个“金鱼”图需要火柴棒的根数为
| A.24 | B.26 | C.28 | D.30 |
用数学归纳法证明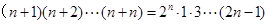 (
(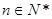 )时,从“
)时,从“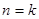 到
到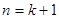 ”左边需增乘的代数式为( )
”左边需增乘的代数式为( )
A.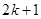 | B.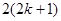 | C.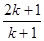 | D. |
在数列{an}中,an=1- +
+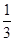 -
-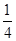 +…+
+…+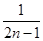 -
-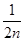 ,则ak+1等于( )
,则ak+1等于( )
A.ak+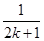 | B.ak+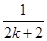 - -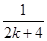 |
C.ak+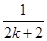 | D.ak+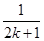 - -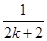 |
分析法又称执果索因法,若用分析法证明:“设a>b>c,且a+b+c=0,求证 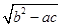 <
<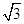 a”索的因应是( )
a”索的因应是( )
| A.a-b>0 | B.a-c>0 |
| C.(a-b)(a-c)>0 | D.(a-b)(a-c)<0 |
用数学归纳法证明“n3+(n+1)3+(n+2)3(n∈N*)能被9整除”,要利用归纳假设证n=k+1时的情况,只需展开( )
| A.(k+3)3 | B.(k+2)3 |
| C.(k+1)3 | D.(k+1)3+(k+2)3 |
 的值依次为
的值依次为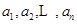 ,其中
,其中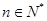 且
且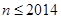 .
.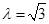 ,写出全部输出结果.
,写出全部输出结果.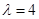 ,记
,记 ,求
,求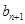 与
与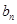 的关系(
的关系(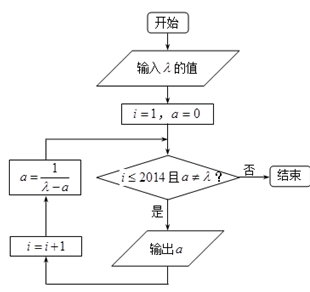
 ,把数列
,把数列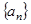 的各项排列成如下的三角形状,
的各项排列成如下的三角形状,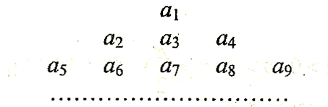
 表示第
表示第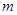 行的第
行的第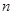 个数,则
个数,则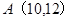 = ( )
= ( )