题目内容
（2012•昌平区一模）一圆形纸片的圆心为点O，点Q是圆内异于O点的一定点，点A是圆周上一点．把纸片折叠使点A与Q重合，然后展平纸片，折痕与OA交于P点．当点A运动时点P的轨迹是（ ）
分析：由线段AQ的垂直平分线，可得|AP|=|PQ|，而|OP|+|PA|=|OA|=R，可得|PO|+|PQ|=R定值＞|OQ|，利用椭圆的定义可知：点P的轨迹是椭圆．
解答：解：如图所示，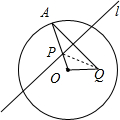
由题意可知：折痕l为线段AQ的垂直平分线，∴|AP|=|PQ|，
而|OP|+|PA|=|OA|=R，∴|PO|+|PQ|=R定值＞|OQ|．
∴当点A运动时点P的轨迹是以点O，D为焦点，长轴长为R的椭圆．
故选B．
由题意可知：折痕l为线段AQ的垂直平分线，∴|AP|=|PQ|，
而|OP|+|PA|=|OA|=R，∴|PO|+|PQ|=R定值＞|OQ|．
∴当点A运动时点P的轨迹是以点O，D为焦点，长轴长为R的椭圆．
故选B．
点评：熟练掌握椭圆的定义、线段的垂直平分线的性质是解题的关键．
练习册系列答案
尖子生新课堂课时作业系列答案
相关题目
（2012•昌平区一模）如图在四棱锥P-ABCD中，底面ABCD是正方形，PA⊥底面ABCD，垂足为点A，PA=AB=2，点M，N分别是PD，PB的中点．