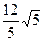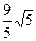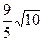题目内容
(本题满分16分)
已知圆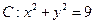 ,点
,点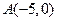 ,直线
,直线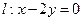 .
.
⑴求与圆 相切,且与直线
相切,且与直线 垂直的直线方程;
垂直的直线方程;
⑵在直线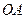 上(
上(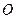 为坐标原点),存在定点
为坐标原点),存在定点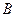 (不同于点
(不同于点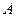 ),满足:对于圆
),满足:对于圆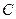 上任一点
上任一点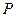 ,都有
,都有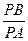 为一常数,试求所有满足条件的点
为一常数,试求所有满足条件的点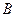 的坐标.
的坐标.
已知圆
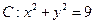 ,点
,点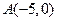 ,直线
,直线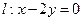 .
.⑴求与圆
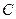 相切,且与直线
相切,且与直线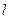 垂直的直线方程;
垂直的直线方程;⑵在直线
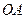 上(
上(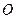 为坐标原点),存在定点
为坐标原点),存在定点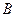 (不同于点
(不同于点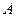 ),满足:对于圆
),满足:对于圆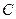 上任一点
上任一点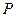 ,都有
,都有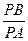 为一常数,试求所有满足条件的点
为一常数,试求所有满足条件的点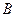 的坐标.
的坐标.
(1)直线方程为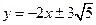
(2)存在点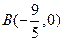 对于圆
对于圆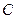 上任一点
上任一点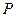 ,都有
,都有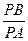 为常数
为常数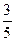 。
。
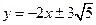
(2)存在点
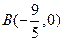 对于圆
对于圆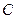 上任一点
上任一点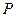 ,都有
,都有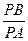 为常数
为常数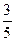 。
。解:⑴设所求直线方程为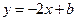 ,即
,即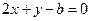 ,
,
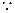 直线与圆相切,∴
直线与圆相切,∴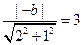 ,得
,得 ,
,
∴所求直线方程为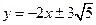 -----------5分
-----------5分
⑵方法1:假设存在这样的点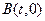 ,
,
当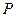 为圆
为圆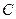 与
与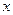 轴左交点
轴左交点 时,
时,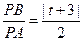 ;
;
当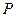 为圆
为圆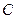 与
与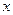 轴右交点
轴右交点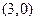 时,
时,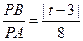 ,
,
依题意,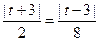 ,解得,
,解得,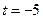 (舍去),或
(舍去),或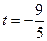 。 -----------------8分
。 -----------------8分
下面证明 点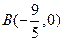 对于圆
对于圆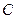 上任一点
上任一点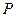 ,都有
,都有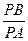 为一常数。
为一常数。
设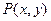 ,则
,则 ,
,
∴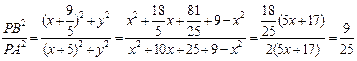 ,
,
从而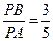 为常数。 -------------15分
为常数。 -------------15分
方法2:假设存在这样的点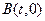 ,使得
,使得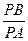 为常数
为常数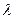 ,则
,则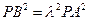 ,
,
∴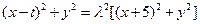 ,将
,将 代入得,
代入得,
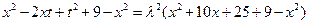 ,即
,即
 对
对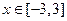 恒成立, ----------------8分
恒成立, ----------------8分
∴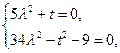 ,解得
,解得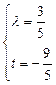 或
或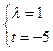 (舍去),
(舍去),
所以存在点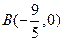 对于圆
对于圆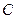 上任一点
上任一点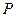 ,都有
,都有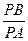 为常数
为常数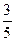 。 ------------15分
。 ------------15分
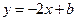 ,即
,即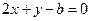 ,
,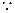 直线与圆相切,∴
直线与圆相切,∴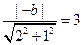 ,得
,得 ,
,∴所求直线方程为
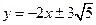 -----------5分
-----------5分⑵方法1:假设存在这样的点
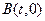 ,
,当
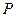 为圆
为圆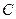 与
与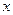 轴左交点
轴左交点 时,
时,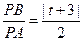 ;
;当
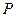 为圆
为圆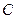 与
与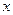 轴右交点
轴右交点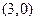 时,
时,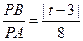 ,
,依题意,
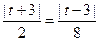 ,解得,
,解得,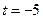 (舍去),或
(舍去),或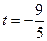 。 -----------------8分
。 -----------------8分下面证明 点
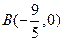 对于圆
对于圆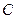 上任一点
上任一点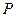 ,都有
,都有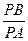 为一常数。
为一常数。设
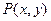 ,则
,则 ,
, ∴
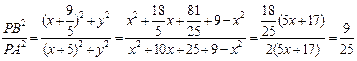 ,
,从而
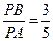 为常数。 -------------15分
为常数。 -------------15分方法2:假设存在这样的点
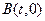 ,使得
,使得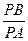 为常数
为常数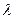 ,则
,则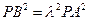 ,
,∴
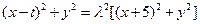 ,将
,将 代入得,
代入得,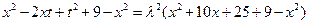 ,即
,即 对
对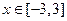 恒成立, ----------------8分
恒成立, ----------------8分∴
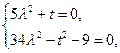 ,解得
,解得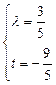 或
或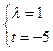 (舍去),
(舍去),所以存在点
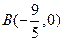 对于圆
对于圆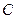 上任一点
上任一点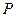 ,都有
,都有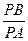 为常数
为常数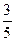 。 ------------15分
。 ------------15分
练习册系列答案
相关题目
 所得的弦长为2,则直线的斜率为( )
所得的弦长为2,则直线的斜率为( )



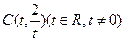 为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点。
为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点。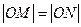 ,求圆C的方程;
,求圆C的方程;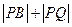 的最小值及此时点P的坐标。
的最小值及此时点P的坐标。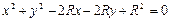 在直角坐标系中的位置特征是 ( )
在直角坐标系中的位置特征是 ( )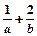 的最小值是________.
的最小值是________. 作直线与圆
作直线与圆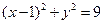 相交于M、N两点,则
相交于M、N两点,则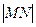 的最小值为( )
的最小值为( )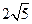
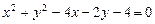 的周长,则mn的取值范围是( )
的周长,则mn的取值范围是( )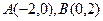 ,实数
,实数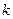 是常数,M,N是圆
是常数,M,N是圆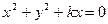 上两个不同点,P是圆
上两个不同点,P是圆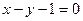 对称,则
对称,则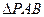 面积的最大值是 ( )
面积的最大值是 ( )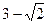
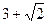
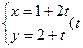 为参数)被圆
为参数)被圆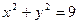 截得的弦长为 ( )
截得的弦长为 ( )