题目内容
已知数列 的前
的前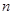 项和
项和 ,则
,则 .
.
 的前
的前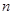 项和
项和 ,则
,则 .
. (
( )
)试题分析:因为根据已知条件可知当n=1时,有

当
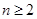 时,则
时,则
经验证当n=1时也适合上式。故可知答案为

点评:解决该试题的关键是能利用数列的前n项和公式与通项公式的关系式:
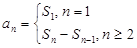 来求解得到。这是很重要的公式,讨论的时候不要忘记验证首项。
来求解得到。这是很重要的公式,讨论的时候不要忘记验证首项。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
 的前
的前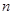 项和
项和 ,则
,则 .
. (
( )
)
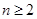 时,则
时,则

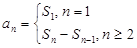 来求解得到。这是很重要的公式,讨论的时候不要忘记验证首项。
来求解得到。这是很重要的公式,讨论的时候不要忘记验证首项。
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案