题目内容
对于数列{an},规定{△an}为数列{an}的一阶差分数列,其中△an=an+1-an(n∈N*);一般地,规定{△kan}为数列{an}的k阶差分数列,其中△kan=△k-1an+1-△k-1an,且k∈N*,k≥2.(Ⅰ)已知数列{an}的通项公式an=
| 5 |
| 2 |
| 13 |
| 2 |
(Ⅱ)若数列{an}的首项a1=1,且满足△2an-an+1+an=-2n(n∈N*),求数列{an}的通项公式;
(Ⅲ)在(Ⅱ)的条件下,记bn=
|
| b2 |
| 2 |
| bn |
| n |
| 17 |
| 12 |
分析:(Ⅰ)根据题意:△an=an+1-an=(n+1)2-(n+1)-n2+n=5n-4,所以△an+1-△an=6.由此能够证明{△an}是等差数列.
(Ⅱ)由△2an-△an+1+an=-2n,知△an+1-△an-△an+1+an=-2n,所以△an-an=2n.由此入手能够求出数列{an}的通项公式.
(Ⅲ)由an=n•2n-1,bn=
=
=
,当n≥2,n∈N*时,
=
=
(
-
),由此入手,能够证明b1+
+…+
<
.
(Ⅱ)由△2an-△an+1+an=-2n,知△an+1-△an-△an+1+an=-2n,所以△an-an=2n.由此入手能够求出数列{an}的通项公式.
(Ⅲ)由an=n•2n-1,bn=
|
|
|
| bn |
| n |
| 1 |
| n(n+2) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
| b2 |
| 2 |
| bn |
| n |
| 17 |
| 12 |
解答:解:(Ⅰ)根据题意:△an=an+1-an=(n+1)2-(n+1)-n2+n=5n-4 (2分)
∴△an+1-△an=6.
∴数列{Dan}是首项为1,公差为5的等差数列.(3分)
(Ⅱ)由△2an-△an+1+an=-2n,∴△an+1-△an-△an+1+an=-2n,?△an-an=2n.(5分)
而△an=an+1-an,∴an+1-2an=2n,∴
-
=
,(6分)
∴数列{
}构成以
为首项,
为公差的等差数列,
即
=
?an=n•2n-1.(7分)
(Ⅲ)由(Ⅱ)知an=n•2n-1,
∴bn=
=
=
(9分)
∴当n≥2,n∈N*时
=
=
(
-
),
∴b1+
+…+
=1+[(
-
)+(
-
)+(
-
)+…+(
-
)+(
-
)]
=1+
(
+
-
-
)<1+
(
+
)=
.
当n=1时,b1=1<
,显然成立.
∴b1+
+…+
<
.(12分)
∴△an+1-△an=6.
∴数列{Dan}是首项为1,公差为5的等差数列.(3分)
(Ⅱ)由△2an-△an+1+an=-2n,∴△an+1-△an-△an+1+an=-2n,?△an-an=2n.(5分)
而△an=an+1-an,∴an+1-2an=2n,∴
| an+1 |
| 2n+1 |
| an |
| 2n |
| 1 |
| 2 |
∴数列{
| an |
| 2n |
| 1 |
| 2 |
| 1 |
| 2 |
即
| an |
| 2n |
| n |
| 2 |
(Ⅲ)由(Ⅱ)知an=n•2n-1,
∴bn=
|
|
|
∴当n≥2,n∈N*时
| bn |
| n |
| 1 |
| n(n+2) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
∴b1+
| b2 |
| 2 |
| bn |
| n |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| n-1 |
| 1 |
| n+1 |
| 1 |
| n |
| 1 |
| n+2 |
=1+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 17 |
| 12 |
当n=1时,b1=1<
| 17 |
| 12 |
∴b1+
| b2 |
| 2 |
| bn |
| n |
| 17 |
| 12 |
点评:第(Ⅰ)题考查等差数列的证明,解题时要注意等差数列性质的合理运用;第(Ⅱ)题考查数列通项公式的求解方法,解题时要注意构造法的合理运用;第(Ⅲ)题考查数列前n项和的证明,解题时要注意裂项求和法的合理运用.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 n2-
n2- n(n∈N*),试证明{△an}是等差数列;
n(n∈N*),试证明{△an}是等差数列;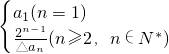 ,求证:b1+
,求证:b1+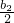 +…+
+…+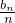 <
<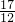 .
.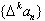 为{an}的k阶差分数列,其中
为{an}的k阶差分数列,其中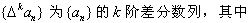
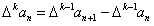 ,且
,且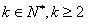 。
。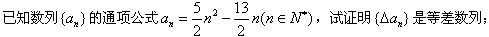
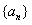 的首项
的首项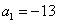 ,且满足
,且满足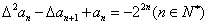 ,求数列
,求数列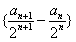 及
及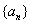 的通项公式;
的通项公式; 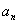 是否存在最小值,若存在求出其最小值,若不存在说明理由。
是否存在最小值,若存在求出其最小值,若不存在说明理由。 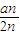 ,求数列{bn}的通项公式;
,求数列{bn}的通项公式; ,求证:c1+
,求证:c1+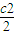 +…+
+…+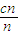 <
<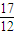 .
.