题目内容
对于数列{an},规定数列{△an}为数列{an}的一阶差分数列,其中△an=an+1-an(n∈N*);一般地,规定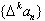 为{an}的k阶差分数列,其中
为{an}的k阶差分数列,其中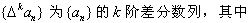
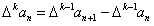 ,且
,且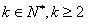 。
。
(1)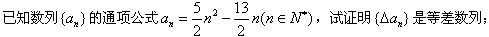
(2)若数列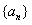 的首项
的首项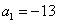 ,且满足
,且满足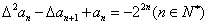 ,求数列
,求数列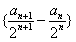 及
及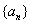 的通项公式;
的通项公式;
(3)在(2)的条件下,判断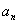 是否存在最小值,若存在求出其最小值,若不存在说明理由。
是否存在最小值,若存在求出其最小值,若不存在说明理由。
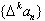 为{an}的k阶差分数列,其中
为{an}的k阶差分数列,其中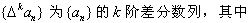
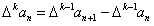 ,且
,且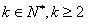 。
。(1)
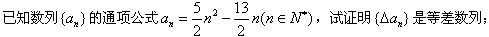
(2)若数列
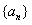 的首项
的首项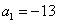 ,且满足
,且满足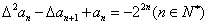 ,求数列
,求数列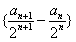 及
及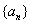 的通项公式;
的通项公式; 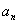 是否存在最小值,若存在求出其最小值,若不存在说明理由。
是否存在最小值,若存在求出其最小值,若不存在说明理由。 解:(1)依题意,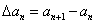 ,
,
∴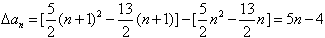 ,
,
∴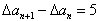 ,
,
∴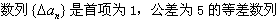 。
。
(2)
∴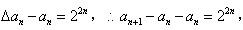
∴
∴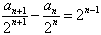 ,
,
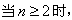
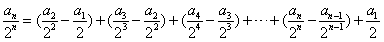
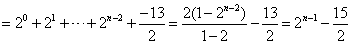 ,
,
∴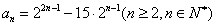 ,
,
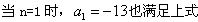 ,
,
∴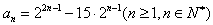 。
。
(3)∵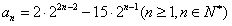 ,
,
令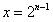 ,则
,则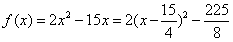 ,
,
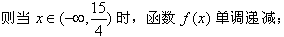 当
当
而 ,
,
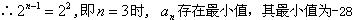 。
。
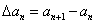 ,
,∴
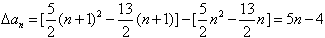 ,
,∴
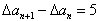 ,
,∴
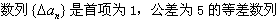 。
。(2)

∴
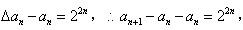
∴

∴
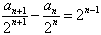 ,
,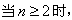
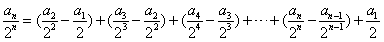
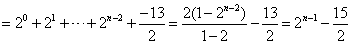 ,
,∴
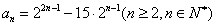 ,
,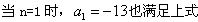 ,
,∴
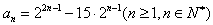 。
。(3)∵
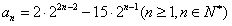 ,
,令
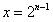 ,则
,则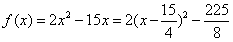 ,
,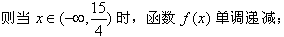 当
当
而
 ,
,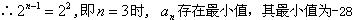 。
。
练习册系列答案
相关题目