题目内容
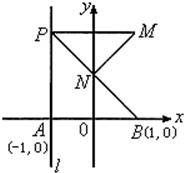（2007•崇文区二模）如图所示，已知A（-1，0），B（1，0），直线l垂直AB于A点，P为l上一动点，点N为线段BP上一点，且满足| BP |
| BN |
| PM |
| AB |
| MN |
| BP |
（Ⅰ）求动点M的轨迹方程C；
（Ⅱ）在上述曲线C内是否存在一点Q，若过点Q的直线与曲线C交于两点E、F，使得以EF为直径的圆都与l相切．若存在，求出点Q的坐标．若不存在，请说明理由．
分析：（I）由
•
=0，
=2
知MN为线段BP的垂直平分线，即|MB|=|MP|，由抛物线定义知点M的轨迹为抛物线，点B为焦点，直线l为准线，进而可得动点M的轨迹方程C；
（Ⅱ）结合（I）中结论，设EF为抛物线的焦点弦，设其中点为H，分别由E、H、F向l作垂线，垂足分别为R、S、T．根据梯形中位线定理可得EF为直径的圆的圆心到直线l的距离等于半径．即以EF为直径的圆必与直线l相切．
| MN |
| BP |
| BP |
| BN |
（Ⅱ）结合（I）中结论，设EF为抛物线的焦点弦，设其中点为H，分别由E、H、F向l作垂线，垂足分别为R、S、T．根据梯形中位线定理可得EF为直径的圆的圆心到直线l的距离等于半径．即以EF为直径的圆必与直线l相切．
解答：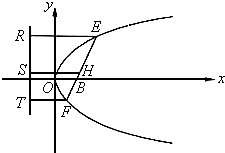
解：（I）由
=2
知点N为BP中点
由
=λ
（λ＞0），知
∥
且点M与B位于l同侧
∵
•
=0，
∴
⊥
由此知MN为线段BP的垂直平分线，
所以应有|MB|=|MP|
由抛物线定义知点M的轨迹为抛物线，点B为焦点，直线l为准线…（8分）
因为A（-1，0），B（1，0），
所以l：x=-1
抛物线方程为y2=4x，即为点M的轨迹方程…（10分）
（II）存在点Q，即为焦点B（1，0）…（11分）
先证明如下：设EF为抛物线的焦点弦，设其中点为H，分别由E、H、F向l作垂线，垂足分别为R、S、T．
由梯形的中位线知：|HS|=
(|ER|+|FT|)=
(|EB|+|FB|)=
|EF|…（13分）
即以EF为直径的圆的圆心到直线l的距离等于半径．
所以以EF为直径的圆必与直线l相切．
所以，存在点Q，其坐标为（1，0）．…（14分）
解：（I）由| BP |
| BN |
由
| PM |
| AB |
| PM |
| AB |
∵
| MN |
| BP |
∴
| MN |
| BP |
由此知MN为线段BP的垂直平分线，
所以应有|MB|=|MP|
由抛物线定义知点M的轨迹为抛物线，点B为焦点，直线l为准线…（8分）
因为A（-1，0），B（1，0），
所以l：x=-1
抛物线方程为y2=4x，即为点M的轨迹方程…（10分）
（II）存在点Q，即为焦点B（1，0）…（11分）
先证明如下：设EF为抛物线的焦点弦，设其中点为H，分别由E、H、F向l作垂线，垂足分别为R、S、T．
由梯形的中位线知：|HS|=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即以EF为直径的圆的圆心到直线l的距离等于半径．
所以以EF为直径的圆必与直线l相切．
所以，存在点Q，其坐标为（1，0）．…（14分）
点评：本题考查的知识点是抛物线的定义及性质，熟练掌握抛物线的定义和性质及直线与圆的位置关系等基本知识点是解答本题的关键．
练习册系列答案
相关题目