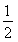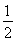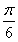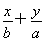题目内容
函数f(x)＝ln x的图像与函数g(x)＝x2－4x＋4的图像的交点个数为( )
A．0 B．1 C．2 D．3
C
【解析】方法一，作出函数f(x)＝ln x，g(x)＝x2－4x＋4的图像如图所示，则两个函数图像的交点个数为2，故选C.
方法二，构造函数φ(x)＝ln x－x2＋4x－4，则φ′(x)＝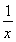
－2x＋4＝－
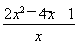.又因为方程2x2－4x－1＝0的大于零的根的是x0＝
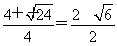，且在(0，x0)上φ′(x)>0，在(x0，＋∞)上φ′(x)<0，所以函数φ(x)至多有两个零点．由于φ(1)＝－1<0，φ(2)＝ln 2>0，φ(4)＝ln 4－4<0，则函数φ(x)有两个不同的零点．故函数f(x)＝ln x的图像与函数g(x)＝x2－4x＋4的图像的交点个数为2.
练习册系列答案
相关题目
一家商场为了确定营销策略，进行了投入促销费用x和商场实际销售额y的试验，得到如下四组数据．
投入促销费用x(万元) | 2 | 3 | 5 | 6 |
商场实际营销额y(万元) | 100 | 200 | 300 | 400 |
(1)在下面的直角坐标系中，画出上述数据的散点图，并据此判断两个变量是否具有较好的线性相关性；
(2)求出x，y之间的回归直线方程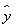
＝
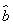x＋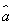
；
(3)若该商场计划营销额不低于600万元，则至少要投入多少万元的促销费用？
