题目内容
已知公差不为零的等差数列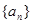 ,满足
,满足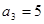 且
且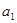 ,
,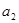 ,
,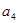 成等比数列.
成等比数列.
(1)求数列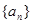 的通项公式;
的通项公式;
(2)设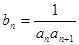 ,求数列
,求数列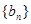 前
前 项的和为
项的和为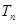 .
.
(1)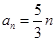 ;(2)
;(2) 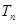
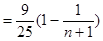 .
.
解析试题分析:(1)设公差不为零的等差数列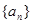 的公差为d(d
的公差为d(d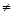 0),首项为
0),首项为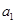 ,则由等差数列的通项公式:
,则由等差数列的通项公式: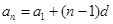 可将
可将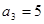 转化为关于
转化为关于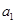 和d的方程,又因为
和d的方程,又因为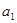 ,
,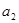 ,
,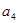 成等比数列
成等比数列 也可转化为关于
也可转化为关于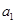 和d的方程,两个方程联立解方程组就可求出
和d的方程,两个方程联立解方程组就可求出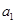 和d的值,代入通项公式:
和d的值,代入通项公式: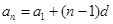 中求得数列的通项公式;(2)由已知知数列
中求得数列的通项公式;(2)由已知知数列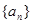 是等差数列,则
是等差数列,则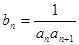 能转化为:
能转化为: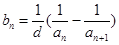 ,这样数列数
,这样数列数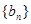 前
前 项的和就可用裂项相消法求和为:
项的和就可用裂项相消法求和为: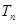
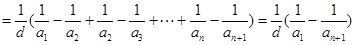 .
.
试题解析:(1)设公差为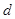 ,则有
,则有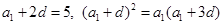 ,又
,又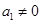
解得: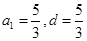 得:
得: 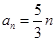 (
(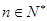 )
)
(2)由题意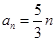 ,
,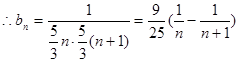
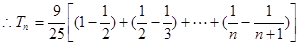
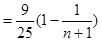
考点:1.等差数列;2.数列求和.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 所有项均为正数,首
所有项均为正数,首 ,且
,且 成等差数列.
成等差数列. 的前n项和为
的前n项和为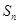 ,若
,若 ,求实数
,求实数 的值.
的值.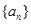 满足:
满足: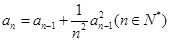
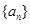 是以常数
是以常数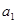 为首项,公差也为
为首项,公差也为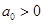 ,求证:
,求证: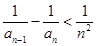 对任意
对任意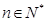 都成立;
都成立;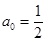 ,求证:
,求证: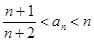 对任意
对任意 的前
的前 项和
项和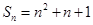 ,
,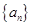 的前n项和
的前n项和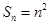 ,数列
,数列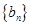 满足
满足 .
.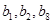 成等比数列,试求
成等比数列,试求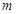 的值;
的值;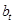 满足
满足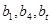 (
(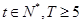 )成等差数列?若存在,请指出符合题意的
)成等差数列?若存在,请指出符合题意的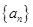 的通项公式为
的通项公式为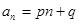 ,其中
,其中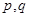 是常数,且
是常数,且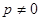 .
.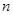 项和为
项和为 ,且
,且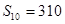 ,
,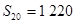 ,试确定
,试确定 的公式.
的公式. 为等差数列,且
为等差数列,且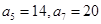 ,数列
,数列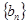 的前
的前 项和为
项和为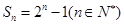 ,
,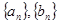 的通项公式;
的通项公式;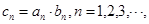 ,求数列
,求数列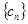 的前
的前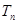 .
.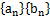 (
(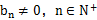 ),满足
),满足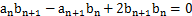 .
.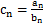 ,求数列
,求数列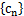 的通项公式;
的通项公式;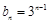 ,求数列
,求数列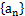 的前n项和
的前n项和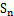
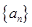 的公差为
的公差为 ,项数是偶数,所有奇数项之和为
,项数是偶数,所有奇数项之和为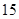 ,所有偶数项之和为
,所有偶数项之和为 ,则这个数列的项数为 ;
,则这个数列的项数为 ;