题目内容
已知向量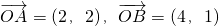 ,在x轴上一点P,使
,在x轴上一点P,使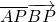 有最小值,则点P 的坐标为
有最小值,则点P 的坐标为
- A.(-3,0)
- B.(2,0)
- C.(3,0)
- D.(4,0)
C
分析:设P(x,0),可得 、
、 含有x的坐标形式,由向量数量积的坐标运算公式得
含有x的坐标形式,由向量数量积的坐标运算公式得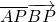 =x2-6x+10,结合二次函数的图象与性质,可得当x=3时
=x2-6x+10,结合二次函数的图象与性质,可得当x=3时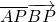 取得最小值1,得到本题答案.
取得最小值1,得到本题答案.
解答:设点P的坐标为(x,0),可得
 =(x-2,-2),
=(x-2,-2), =(x-4,-1).
=(x-4,-1).
因此,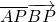 =(x-4)(x-2)+2=x2-6x+10=(x-3)2+1.
=(x-4)(x-2)+2=x2-6x+10=(x-3)2+1.
∵二次函数y=(x-3)2+1,当x=3时取得最小值为1
∴当x=3时,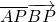 取得最小值1,此时P(3,0).
取得最小值1,此时P(3,0).
故选:C
点评:本题给出向量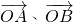 的坐标,求在x轴上一点P,使
的坐标,求在x轴上一点P,使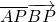 有最小值.着重考查了向量数量积的坐标运算公式和二次函数的性质等知识,属于基础题.
有最小值.着重考查了向量数量积的坐标运算公式和二次函数的性质等知识,属于基础题.
分析:设P(x,0),可得
 、
、 含有x的坐标形式,由向量数量积的坐标运算公式得
含有x的坐标形式,由向量数量积的坐标运算公式得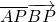 =x2-6x+10,结合二次函数的图象与性质,可得当x=3时
=x2-6x+10,结合二次函数的图象与性质,可得当x=3时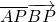 取得最小值1,得到本题答案.
取得最小值1,得到本题答案.解答:设点P的坐标为(x,0),可得
 =(x-2,-2),
=(x-2,-2), =(x-4,-1).
=(x-4,-1).因此,
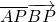 =(x-4)(x-2)+2=x2-6x+10=(x-3)2+1.
=(x-4)(x-2)+2=x2-6x+10=(x-3)2+1.∵二次函数y=(x-3)2+1,当x=3时取得最小值为1
∴当x=3时,
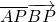 取得最小值1,此时P(3,0).
取得最小值1,此时P(3,0).故选:C
点评:本题给出向量
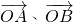 的坐标,求在x轴上一点P,使
的坐标,求在x轴上一点P,使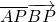 有最小值.着重考查了向量数量积的坐标运算公式和二次函数的性质等知识,属于基础题.
有最小值.着重考查了向量数量积的坐标运算公式和二次函数的性质等知识,属于基础题. 
练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
 )且方向向量为
)且方向向量为 的直线l交椭圆C于A、B两点,交x轴于M点,又
的直线l交椭圆C于A、B两点,交x轴于M点,又 .
.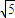 )且方向向量为
)且方向向量为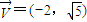 的直线l交椭圆C于A、B两点,交x轴于M点,又
的直线l交椭圆C于A、B两点,交x轴于M点,又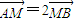 .
.