题目内容
（理科）已知椭圆C的中心在原点，焦点在x轴上，一条经过点（3，-
）且方向向量为
的直线l交椭圆C于A、B两点，交x轴于M点，又
．（1）求直线l方程；
（2）求椭圆C长轴长取值的范围．
【答案】分析：（1）由条件：一条经过点（3，-
）且方向向量为
，可得直线的斜率，进而可求直线l方程；
（2）将直线与椭圆方程联立，利用
．可得几何量之间的关系，借助于直线l交椭圆C于A、B两点，从而有判别式大于0，故可求椭圆C长轴长取值的范围．
解答：解：（1）直线l过点（3，-
）且方向向量为
∴
化简为：
…（4分）
（2）设直线
交于两点A（x1，y1），B（x2，y2），和x轴交于M（1，0）
由
…（7分）
将
…①
由韦达定理知：
由②2/③知：32b2=（4b2+5a2）（a2-1）…（10分）
化为
…④
对方程①求判别式，且由△＞0，即
化简为：5a2+4b2＞5…⑤
由④式代入⑤可知：
，
又椭圆的焦点在x轴上，则a2＞b2，由④知：
．
因此所求椭圆长轴长2a范围为
．
点评：本题以椭圆为载体，考查直线与椭圆的位置关系，关键是直线与椭圆方程的联立，利用韦达定理可解．
）且方向向量为，可得直线的斜率，进而可求直线l方程； （2）将直线与椭圆方程联立，利用
．可得几何量之间的关系，借助于直线l交椭圆C于A、B两点，从而有判别式大于0，故可求椭圆C长轴长取值的范围．解答：解：（1）直线l过点（3，-
）且方向向量为∴化简为：
…（4分）（2）设直线
交于两点A（x1，y1），B（x2，y2），和x轴交于M（1，0）
由
…（7分）将
…①由韦达定理知：
由②2/③知：32b2=（4b2+5a2）（a2-1）…（10分）
化为
…④对方程①求判别式，且由△＞0，即
化简为：5a2+4b2＞5…⑤
由④式代入⑤可知：
，又椭圆的焦点在x轴上，则a2＞b2，由④知：
．因此所求椭圆长轴长2a范围为
．点评：本题以椭圆为载体，考查直线与椭圆的位置关系，关键是直线与椭圆方程的联立，利用韦达定理可解．
练习册系列答案
阅读快车系列答案
相关题目
）且方向向量为
的直线l交椭圆C于A、B两点，交x轴于M点，又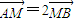
．
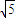）且方向向量为
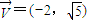的直线l交椭圆C于A、B两点，交x轴于M点，又
．
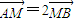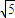）且方向向量为
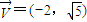的直线l交椭圆C于A、B两点，交x轴于M点，又
．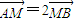