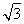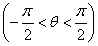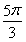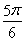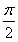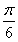Question

已知函数f(x)＝2sin2 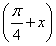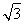－cos 2x－1(x∈R)．

(1)若函数h(x)＝f(x＋t)的图象关于点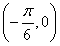对称，且t∈(0，π)，求t的值；

(2)设p：x∈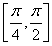，q：|f(x)－m|＜3，若p是q的充分不必要条件，求实数m的取值范围．

 

Answer 1

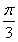（1）t＝或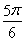.（2）(－1,4)

【解析】(1)f(x)＝2sin2 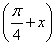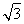－cos 2x－1

＝1－cos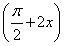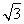－cos 2x－1＝2sin ，

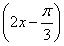∴h(x)＝f(x＋t)＝2sin 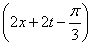.∴h(x)的对称中心为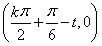，k∈Z，

又已知点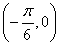为h(x)的图象的一个对称中心，∴t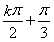＝，k∈Z.

而t∈(0，π)，∴t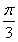＝或.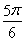

(2)若p成立，即x∈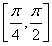时，

2x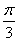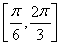－∈，f(x)∈[1,2]，

由|f(x)－m|＜3⇒m－3＜f(x)＜m＋3，

因为p是q的充分不必要条件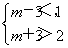，⇒－1＜m＜4.

故m的取值范围为(－1,4)．