题目内容
已知动点 与定点
与定点 的距离和它到直线
的距离和它到直线 的距离之比是常数
的距离之比是常数 ,记
,记 的轨迹为曲线
的轨迹为曲线 .
.
(I)求曲线 的方程;
的方程;
(II)设直线 与曲线
与曲线 交于
交于 两点,点
两点,点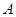 关于
关于 轴的对称点为
轴的对称点为 ,试问:当
,试问:当 变化时,直线
变化时,直线 与
与 轴是否交于一个定点?若是,请写出定点的坐标,并证明你的结论;若不是,请说明理由.
轴是否交于一个定点?若是,请写出定点的坐标,并证明你的结论;若不是,请说明理由.
【答案】
(I)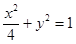 ;(II)对于任意的
;(II)对于任意的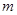 ,直线
,直线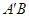 与
与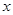 轴交于定点
轴交于定点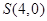 .
.
【解析】
试题分析:(I)找出题中的相等关系,列出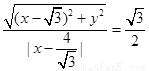 ,化简即得曲线
,化简即得曲线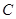 的方程;(II)将直线方程代入曲线
的方程;(II)将直线方程代入曲线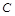 方程,消去
方程,消去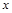 得
得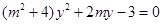 ,记
,记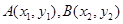 ,则
,则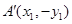 ,且
,且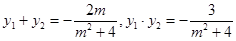 .特别地,令
.特别地,令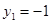 ,则
,则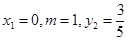 .此时
.此时 ,直线
,直线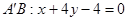 与
与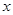 轴的交点为
轴的交点为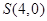 .若直线
.若直线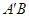 与
与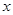 轴交于一个定点,则定点只能为
轴交于一个定点,则定点只能为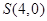 .再证明对于任意的
.再证明对于任意的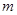 ,直线
,直线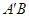 与
与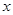 轴交于定点
轴交于定点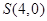 ,可利用直线的两点式方程结合分析法.
,可利用直线的两点式方程结合分析法.
试题解析:(I)设 是点
是点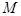 到直线
到直线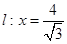 的距离,根据题意,点
的距离,根据题意,点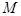 的轨迹就是集合
的轨迹就是集合
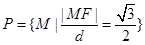
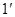
由此得
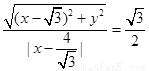
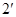
将上式两边平方,并化简得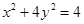
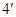
即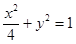 ,所以曲线
,所以曲线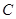 的方程为
的方程为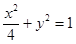
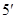
(II)由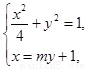 得
得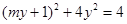 ,即
,即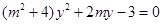 .
. 
记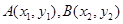 ,
,
则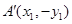 ,且
,且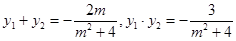 .
. 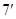
特别地,令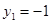 ,则
,则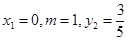 .
.
此时 ,直线
,直线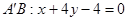 与
与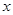 轴的交点为
轴的交点为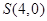 .
. 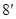
若直线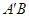 与
与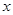 轴交于一个定点,则定点只能为
轴交于一个定点,则定点只能为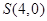 .
.
以下证明对于任意的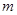 ,直线
,直线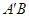 与
与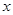 轴交于定点
轴交于定点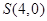 .
.
事实上,经过点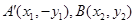 的直线方程为
的直线方程为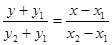 .
.
令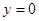 ,得
,得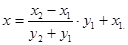 只需证
只需证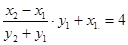 ,
, 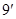
即证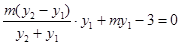 ,即证
,即证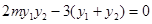 .
. 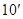
因为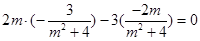 ,
, 
所以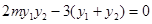 成立.
成立.
这说明,当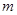 变化时,直线
变化时,直线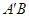 与
与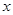 轴交于定点
轴交于定点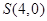 .
…
.
…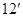
考点:1、曲线方程求法;2、直线与圆锥曲线位置关系;3、定点问题.

练习册系列答案
相关题目
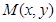 到定点
到定点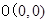 与到定点
与到定点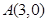 的距离之比为
的距离之比为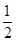 .
. 的轨迹C的方程,并指明曲线C的轨迹;
的轨迹C的方程,并指明曲线C的轨迹;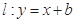 ,若曲线C上恰有三个点到直线的距离为1,求实数的值。
,若曲线C上恰有三个点到直线的距离为1,求实数的值。