题目内容
【题目】已知直线![]() ,且与坐标轴形成的三角形面积为
,且与坐标轴形成的三角形面积为![]() .求:
.求:
(1)求证:不论![]() 为何实数,直线
为何实数,直线![]() 过定点P;
过定点P;
(2)分别求![]() 和
和![]() 时,所对应的直线条数;
时,所对应的直线条数;
(3)针对![]() 的不同取值,讨论集合
的不同取值,讨论集合![]() 直线
直线![]() 经过P,且与坐标轴围成的三角形面积为
经过P,且与坐标轴围成的三角形面积为![]() 中的元素个数.
中的元素个数.
【答案】(1)定点![]() ,见解析;(2)
,见解析;(2)![]() 时,2条直线,
时,2条直线,![]() 时,4条直线;(3)①
时,4条直线;(3)①![]() 时,2条直线; ②
时,2条直线; ②![]() 时,3条直线; ③
时,3条直线; ③![]() 时,4条直线.
时,4条直线.
【解析】
(1)直线方程化为![]() ,令
,令![]() 求得直线
求得直线![]() 所过的定点;
所过的定点;
(2)由题意知直线的斜率存在且不为0,设出直线方程,求出直线与![]() 轴的交点,计算对应三角形的面积,由此求得直线条数;
轴的交点,计算对应三角形的面积,由此求得直线条数;
(3)由题意得![]() ,讨论
,讨论![]() 和
和![]() 时方程对应的实数根,从而求出对应直线的条数,即可得出集合
时方程对应的实数根,从而求出对应直线的条数,即可得出集合![]() 直线经过P且与坐标轴围成的三角形面积为
直线经过P且与坐标轴围成的三角形面积为![]() 中元素的个数.
中元素的个数.
(1)直线![]() 可化为
可化为![]() ,
,
令![]() ,解得
,解得![]() ,
,
∴不论![]() 为何实数,直线
为何实数,直线![]() 过定点
过定点![]() .
.
(2)由题意知,直线的斜率![]() 存在,且
存在,且![]() ,
,
设直线方程为![]() ,则直线与
,则直线与![]() 轴的交点为
轴的交点为![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ;
;
∴![]() 的面积为
的面积为![]() ;
;
令![]() ,得
,得![]() ,
,![]() 时,方程化为
时,方程化为![]() ,
,
解得![]() ,有两个正根,即有两条直线;
,有两个正根,即有两条直线;
![]() 时,方程化为
时,方程化为![]() ,
,![]() ,方程无实数根,即无直线;
,方程无实数根,即无直线;
综上知,![]() 时有两条直线;
时有两条直线;
令![]() ,得
,得![]() ,
,![]() 时,方程化为
时,方程化为![]() ,
,
解得![]() ,有两个正根,即有两条直线;
,有两个正根,即有两条直线;
![]() 时,方程化为
时,方程化为![]() ,解得
,解得![]() ,有两个负根,即有两条直线;
,有两个负根,即有两条直线;
综上知,![]() 时有四条直线;
时有四条直线;
(3)由题意得,![]() ,
,![]() 时,方程化为
时,方程化为![]() ,
,
解得![]() ,有两个正根,即有两条直线;
,有两个正根,即有两条直线;
![]() 时,方程化为
时,方程化为![]() ,
,![]() ,
,![]() 时,
时,
![]() ,方程无实数根,此时无直线;
,方程无实数根,此时无直线;
![]() 时,
时,![]() ,方程有一负根
,方程有一负根![]() ,此时有一条直线;
,此时有一条直线;
![]() 时,
时,![]() ,解得
,解得![]() ,方程有两负根,即有两条直线;
,方程有两负根,即有两条直线;
综上知,![]() 时有两条直线;
时有两条直线;![]() 时有三条直线,
时有三条直线,![]() 时有4条直线;
时有4条直线;
所以![]() 时,集合
时,集合![]() 直线经过P且与坐标轴围成的三角形面积为
直线经过P且与坐标轴围成的三角形面积为![]() 中的元素有2个;
中的元素有2个;
![]() 时,集合
时,集合![]() 直线经过P且与坐标轴围成的三角形面积为
直线经过P且与坐标轴围成的三角形面积为![]() 中的元素有3个;
中的元素有3个;
![]() 时,集合
时,集合![]() 直线经过P且与坐标轴围成的三角形面积为
直线经过P且与坐标轴围成的三角形面积为![]() 中的元素有4个.
中的元素有4个.

 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案【题目】“有黑扫黑、无黑除恶、无恶治乱”,维护社会稳定和和平发展.扫黑除恶期间,大量违法分子主动投案,某市公安机关对某月连续7天主动投案的人员进行了统计,![]() 表示第
表示第![]() 天主动投案的人数,得到统计表格如下:
天主动投案的人数,得到统计表格如下:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 3 | 4 | 5 | 5 | 5 | 6 | 7 |
(1)若![]() 与
与![]() 具有线性相关关系,请根据上表提供的数据,用最小二乘法求出
具有线性相关关系,请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)判定变量![]() 与
与![]() 之间是正相关还是负相关.(写出正确答案,不用说明理由)
之间是正相关还是负相关.(写出正确答案,不用说明理由)
(3)预测第八天的主动投案的人数(按四舍五入取到整数).
参考公式: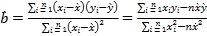 ,
, ![]() ./span>
./span>
【题目】已知抛物线C:y2=2px(p>0)与圆![]() 无公共点,过抛物线C上一点M作圆D的两条切线,切点分别为E,F,当点M在抛物线C上运动时,直线EF都不通过的点构成一个区域,求这个区域的面积的取值范围.
无公共点,过抛物线C上一点M作圆D的两条切线,切点分别为E,F,当点M在抛物线C上运动时,直线EF都不通过的点构成一个区域,求这个区域的面积的取值范围.
【题目】为研究男、女生的身高差异,现随机从高二某班选出男生、女生各10人,并测量他们的身高,测量结果如下(单位:厘米):
男:164 178 174 185 170 158 163 165 161 170
女:165 168 156 170 163 162 158 153 169 172
(1)根据测量结果完成身高的茎叶图(单位:厘米),并分别求出男、女生身高的平均值.
(2)请根据测量结果得到20名学生身高的中位数![]() (单位:厘米),将男、女生身高不低于
(单位:厘米),将男、女生身高不低于![]() 和低于
和低于![]() 的人数填入下表中,并判断是否有
的人数填入下表中,并判断是否有![]() 的把握认为男、女生身高有差异?
的把握认为男、女生身高有差异?
人数 | 男生 | 女生 |
身高 | ||
身高 |
参照公式:![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(3)若男生身高低于165厘米为偏矮,不低于165厘米且低于175厘米为正常,不低于175厘米为偏高.假设可以用测量结果的频率代替概率,试求从高二的男生中任意选出2人,恰有1人身高属于正常的概率.
【题目】为研究男、女生的身高差异,现随机从高二某班选出男生、女生各10人,并测量他们的身高,测量结果如下(单位:厘米):
男:164 178 174 185 170 158 163 165 161 170
女:165 168 156 170 163 162 158 153 169 172
(1)根据测量结果完成身高的茎叶图(单位:厘米),并分别求出男、女生身高的平均值.

(2)请根据测量结果得到20名学生身高的中位数![]() (单位:厘米),将男、女生身高不低于
(单位:厘米),将男、女生身高不低于![]() 和低于
和低于![]() 的人数填入下表中,并判断是否有
的人数填入下表中,并判断是否有![]() 的把握认为男、女生身高有差异?
的把握认为男、女生身高有差异?
人数 | 男生 | 女生 |
身高 | ||
身高 |
参照公式:![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | .024 | 6.635 | 7.879 | 10.828 |
(3)若男生身高低于165厘米为偏矮,不低于165厘米且低于175厘米为正常,不低于175厘米为偏高.假设可以用测量结果的频率代替概率,试求从高二的男生中任意选出2人,恰有1人身高属于正常的概率.