题目内容
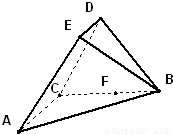
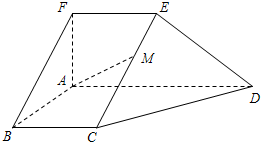 如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,AF=AB=BC=FE=
如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,AF=AB=BC=FE=| 1 |
| 3 |
(Ⅰ)求异面直线BF与DE所成角的余弦值;
(Ⅱ)在线段CE上是否存在点M,使得直线AM与平面CDE所成角的正弦值为
| ||
| 3 |
分析:建立如图的空间坐标系,给出相应点的坐标,
(Ⅰ)求出异面直线BF与DE的方向向量,利用数量积公式的变形形式求两向量的夹角即可.
(Ⅱ)假设在线段CE上存在点M,使得直线AM与平面CDE所成角的正弦值为
,求出直线的方向向量与平面的法向量,利用公式建立方程,若能求出符合条件的参数的值则说明存在,否则说明不存在.
(Ⅰ)求出异面直线BF与DE的方向向量,利用数量积公式的变形形式求两向量的夹角即可.
(Ⅱ)假设在线段CE上存在点M,使得直线AM与平面CDE所成角的正弦值为
| ||
| 3 |
解答: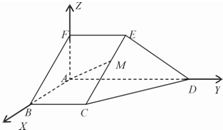 解:建立如图所示的直角坐标系,不妨设AB=1
解:建立如图所示的直角坐标系,不妨设AB=1
则B(1,0,0),C(1,1,0),D(0,3,0),
F(0,0,1),E(0,1,1)
(Ⅰ)
=(-1,0,1),
=(0,-2,1)cos<
,
>=
=
=
∴异面直线BF与DE所成角的余弦值为
.
(Ⅱ)设平面CDE的一个法向量为
=(x,y,z)
=(-1,2,0),
=(0,-2,1)
∵
•
=0
•
=0
∴
令y=1,得x=z=2,∴
=(2,1,2)
设存在点M(p,q,r)满足条件,由
=λ
得
p=1-λ,q=1,r=λ即M(1-λ,1,λ)
∴
=(1-λ,1,λ)
∵直线AM与平面CDE所成角的正弦值为
∴|cos<
,
>|=
,
=
,得λ
故当点M为CE中点时,直线AM与平面CDE所成角的正弦值为
 解:建立如图所示的直角坐标系,不妨设AB=1
解:建立如图所示的直角坐标系,不妨设AB=1则B(1,0,0),C(1,1,0),D(0,3,0),
F(0,0,1),E(0,1,1)
(Ⅰ)
| BF |
| DE |
| BF |
| DE |
| ||||
|
|
| 1 | ||||
|
| ||
| 10 |
∴异面直线BF与DE所成角的余弦值为
| ||
| 10 |
(Ⅱ)设平面CDE的一个法向量为
| n |
| CD |
| DE |
∵
| CD |
| n |
| DE |
| n |
∴
|
令y=1,得x=z=2,∴
| n |
设存在点M(p,q,r)满足条件,由
| CM |
| CE |
p=1-λ,q=1,r=λ即M(1-λ,1,λ)
∴
| AM |
∵直线AM与平面CDE所成角的正弦值为
| ||
| 3 |
∴|cos<
| AM |
| n |
| ||
| 3 |
|
| ||||
|
|
| ||
| 3 |
| 1 |
| 2 |
故当点M为CE中点时,直线AM与平面CDE所成角的正弦值为
| ||
| 3 |
点评:本题考查用空间向量求异面直线所成的角及直线与平面所成的角,及坐标运算等知识,考查数形结合、化归转化的数学思想和方法,以及空间想象能力、推理论证能力和运算求解能力,求线面角时由于直线的方向向量与平面的法向量的夹角的余弦值与线面角的正弦值相等,解题时易由于记忆不准把向量的夹角当成线面角导致出错,对规律性的内容要理解到位,掌握精准.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
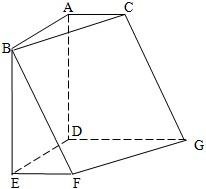 如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG.且AB=AD=DE=DG=2,AC=EF=1.
如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG.且AB=AD=DE=DG=2,AC=EF=1. 如图,在五面体ABCDE中,平面BCD⊥平面ABC,DC=DB=
如图,在五面体ABCDE中,平面BCD⊥平面ABC,DC=DB=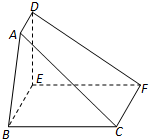 如图,在五面体ABC-DEF中,四边形BCFE 是矩形,DE⊥平面BCFE.
如图,在五面体ABC-DEF中,四边形BCFE 是矩形,DE⊥平面BCFE. ,AC=BC=2ED=2,AC⊥BC,且ED∥AC
,AC=BC=2ED=2,AC⊥BC,且ED∥AC  ,求二面角F-AE-B的余弦值.
,求二面角F-AE-B的余弦值.