题目内容
如图,在五面体ABCDE中,平面BCD⊥平面ABC,DC=DB= ,AC=BC=2ED=2,AC⊥BC,且ED∥AC
,AC=BC=2ED=2,AC⊥BC,且ED∥AC (1)求证:平面ABE⊥平面ABC
(2)在线段BC上有一点F,且
 ,求二面角F-AE-B的余弦值.
,求二面角F-AE-B的余弦值.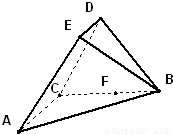
【答案】分析:(1)取BC中点O,AB中点M,连接DO、OM、EM,可证出四边形DOME是平行四边形,得EM∥DO.接下来可以证明EM⊥平面ABC,结合EM?平面ABE,可得平面ABE⊥平面ABC;
(2)以O为原点,分别以OM、OB、OD所在直线为x、y、z轴,建立如图坐标系,得出图中各点的坐标,得 =(2,-
=(2,- ,0),
,0),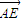 =(-1,1,
=(-1,1,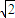 ),利用垂直向量数量积为0建立方程组,解之算出平面FAE的法向量为
),利用垂直向量数量积为0建立方程组,解之算出平面FAE的法向量为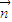 =(1,-
=(1,- ,-
,-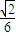 ).最后结合
).最后结合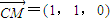 为平面ABE的法向量,利用空间两个向量的夹角公式加以计算,即可算出二面角F-AE-B的余弦值.
为平面ABE的法向量,利用空间两个向量的夹角公式加以计算,即可算出二面角F-AE-B的余弦值.
解答:解:(1)取BC中点O,AB中点M,连接DO、OM、EM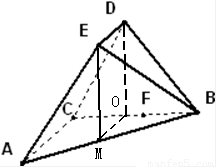
∵DO是等腰△BCD底边上的中线,∴DO⊥BC
∵平面BCD⊥平面ABC,平面BCD∩平面ABC=BC,DO?平面BCD
∴DO⊥平面ABC,
∵OM是△ABC的中位线,∴OM∥AC且OM= AC
AC
∵ED∥AC且ED= AC,∴OM∥ED,得四边形DOME是平行四边形
AC,∴OM∥ED,得四边形DOME是平行四边形
∴EM∥DO,结合DO⊥平面ABC,得EM⊥平面ABC,
∵EM?平面ABE,∴平面ABE⊥平面ABC
(2)以O为原点,分别以OM、OB、OD所在直线为x、y、z轴,建立如图坐标系,
可得B(0,1,0),F(0, ,0),C(0,-1,0),A(2,-1,0)
,0),C(0,-1,0),A(2,-1,0)
D(0,0,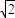 ),E(1,0,
),E(1,0,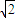 ),M(1,0,0)
),M(1,0,0)
∴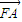 =(2,-
=(2,- ,0),
,0),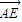 =(-1,1,
=(-1,1,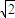 )
)
设平面FAE的一个法向量为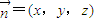
由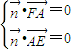 得
得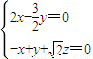 ,
,
令x=1,得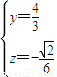 ,∴
,∴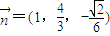
又∵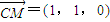 ,
,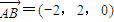 ,
,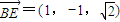 ,
,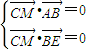
∴ 为平面ABE的一个法向量
为平面ABE的一个法向量
得cos<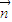 ,
,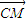 >=
>= =
=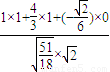 =
=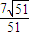 ,
,
又∵二面角F-AE-B为为锐二面角,
∴二面角F-AE-B的余弦值为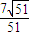 …(12分)
…(12分)
点评:本题给特殊四棱锥,求证面面垂直并求锐二面角的余弦之值,着重考查了平面与平面垂直的判定、空间坐标系的建立和二面角的平面角及求法等知识,属于中档题.
(2)以O为原点,分别以OM、OB、OD所在直线为x、y、z轴,建立如图坐标系,得出图中各点的坐标,得
 =(2,-
=(2,- ,0),
,0),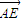 =(-1,1,
=(-1,1,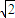 ),利用垂直向量数量积为0建立方程组,解之算出平面FAE的法向量为
),利用垂直向量数量积为0建立方程组,解之算出平面FAE的法向量为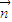 =(1,-
=(1,- ,-
,-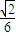 ).最后结合
).最后结合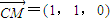 为平面ABE的法向量,利用空间两个向量的夹角公式加以计算,即可算出二面角F-AE-B的余弦值.
为平面ABE的法向量,利用空间两个向量的夹角公式加以计算,即可算出二面角F-AE-B的余弦值.解答:解:(1)取BC中点O,AB中点M,连接DO、OM、EM

∵DO是等腰△BCD底边上的中线,∴DO⊥BC
∵平面BCD⊥平面ABC,平面BCD∩平面ABC=BC,DO?平面BCD
∴DO⊥平面ABC,
∵OM是△ABC的中位线,∴OM∥AC且OM=
 AC
AC∵ED∥AC且ED=
 AC,∴OM∥ED,得四边形DOME是平行四边形
AC,∴OM∥ED,得四边形DOME是平行四边形∴EM∥DO,结合DO⊥平面ABC,得EM⊥平面ABC,
∵EM?平面ABE,∴平面ABE⊥平面ABC
(2)以O为原点,分别以OM、OB、OD所在直线为x、y、z轴,建立如图坐标系,

可得B(0,1,0),F(0,
 ,0),C(0,-1,0),A(2,-1,0)
,0),C(0,-1,0),A(2,-1,0)D(0,0,
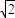 ),E(1,0,
),E(1,0,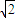 ),M(1,0,0)
),M(1,0,0)∴
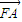 =(2,-
=(2,- ,0),
,0),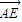 =(-1,1,
=(-1,1,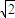 )
)设平面FAE的一个法向量为
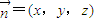
由
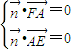 得
得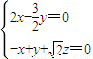 ,
,令x=1,得
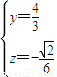 ,∴
,∴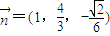
又∵
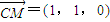 ,
,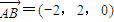 ,
,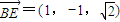 ,
,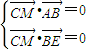
∴
 为平面ABE的一个法向量
为平面ABE的一个法向量得cos<
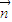 ,
,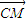 >=
>= =
=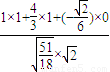 =
=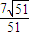 ,
,又∵二面角F-AE-B为为锐二面角,
∴二面角F-AE-B的余弦值为
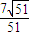 …(12分)
…(12分)点评:本题给特殊四棱锥,求证面面垂直并求锐二面角的余弦之值,着重考查了平面与平面垂直的判定、空间坐标系的建立和二面角的平面角及求法等知识,属于中档题.

练习册系列答案
相关题目
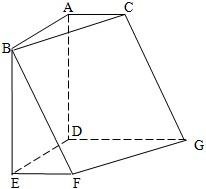 如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG.且AB=AD=DE=DG=2,AC=EF=1.
如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG.且AB=AD=DE=DG=2,AC=EF=1. 如图,在五面体ABCDE中,平面BCD⊥平面ABC,DC=DB=
如图,在五面体ABCDE中,平面BCD⊥平面ABC,DC=DB=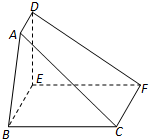 如图,在五面体ABC-DEF中,四边形BCFE 是矩形,DE⊥平面BCFE.
如图,在五面体ABC-DEF中,四边形BCFE 是矩形,DE⊥平面BCFE.