题目内容
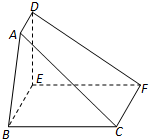如图，在五面体ABC-DEF中，四边形BCFE 是矩形，DE⊥平面BCFE．求证：（1）BC⊥平面ABED；
（2）CF∥AD．
分析：（1）证明BC⊥平面ABED，即可证明BC垂直于平面ABED内的两相交直线；
（2）由线面平行的性质定理，即可得证CF∥AD．
（2）由线面平行的性质定理，即可得证CF∥AD．
解答：证：（1）因为DE⊥平面BCFE，BC?平面BCFE，
所以BC⊥DE．
因为四边形BCFE 是矩形，
所以BC⊥BE．
因为DE?平面ABED，BE?平面ABED，且DE∩BE=E，
所以BC⊥平面ABED．
（2）因为四边形BCFE 是矩形，所以CF∥BE，
因为CF?平面ABED，BE?平面ABED，
所以CF∥平面ABED．
因为CF?平面ACFD，平面ACFD∩平面ABED=AD，
所以CF∥AD．
所以BC⊥DE．
因为四边形BCFE 是矩形，
所以BC⊥BE．
因为DE?平面ABED，BE?平面ABED，且DE∩BE=E，
所以BC⊥平面ABED．
（2）因为四边形BCFE 是矩形，所以CF∥BE，
因为CF?平面ABED，BE?平面ABED，
所以CF∥平面ABED．
因为CF?平面ACFD，平面ACFD∩平面ABED=AD，
所以CF∥AD．
点评：本题考查直线与平面垂直的判定定理以及线面平行的性质定理，考查逻辑思维能力，空间想象能力，是中档题．
练习册系列答案
相关题目
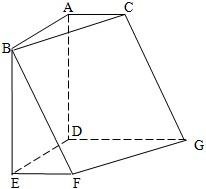如图，在六面体ABCDEFG中，平面ABC∥平面DEFG，AD⊥平面DEFG，AB⊥AC，ED⊥DG，EF∥DG．且AB=AD=DE=DG=2，AC=EF=1．
如图，在五面体ABCDE中，平面BCD⊥平面ABC，DC=DB=
，AC=BC=2ED=2，AC⊥BC，且ED∥AC 
，求二面角F-AE-B的余弦值．
