Question

已知偶函数f（x）在[0，+∞]上为增函数，且f（x-1）＞f（3-2x），求x的取值范围________．

Answer 1

分析：利用函数f（x）的奇偶性及在[0，+∞]上的单调性，
可把f（x-1）＞f（3-2x）转化为关于x-1与3-2x的不等式，从而可以求解．
解答：因为偶函数f（x）在[0，+∞]上为增函数，
所以f（x-1）＞f（3-2x）?f（|x-1|）＞f（|3-2x|）?|x-1|＞|3-2x|，
两边平方并化简得3x²-10x+8＜0，
解得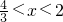，所以x的取值范围为 （）．
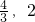故答案为：（）．
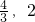点评：本题为函数奇偶性及单调性的综合考查．解决本题的关键是利用性质去掉符号“f”，转化为关于x-1与3-2x的不等式求解．