题目内容
6.已知a是实数,方程4ax2-(4a+2)x+5a+1=0在区间[2,+∞)上至少有一个实根,则实数a的取值范围为(0,$\frac{3}{13}$].分析 对函数类型和根的个数进行讨论,列出不等式解出.
解答 解:令f(x)=4ax2-(4a+2)x+5a+1,
(1)若4a=0,即a=0,则f(x)=-2x+1,
∴f(x)的零点为x=$\frac{1}{2}$∉[2,+∞).
(2)若4a≠0,即a≠0时,f(x)为二次函数,
①若f(x)在区间[2,+∞)上只有一个实根,
若△=0,即(4a+2)2-16a(5a+1)=0,解得a=±$\frac{1}{4}$,
则$\frac{4a+2}{8a}≥2$,无解.
若△>0,即(4a+2)2-16a(5a+1)>0,解得-$\frac{1}{4}$<a<$\frac{1}{4}$且a≠0.
则$\left\{\begin{array}{l}{4a>0}\\{f(2)≤0}\end{array}\right.$或$\left\{\begin{array}{l}{4a<0}\\{f(2)≥0}\end{array}\right.$,
即$\left\{\begin{array}{l}{4a>0}\\{16a-2(4a+2)+5a+1≤0}\end{array}\right.$或$\left\{\begin{array}{l}{4a<0}\\{16a-2(4a+2)+5a+1≥0}\end{array}\right.$,
解得0<a$≤\frac{3}{13}$
②若f(x)在区间[2,+∞)上有两个实根,
则$\left\{\begin{array}{l}{4a>0}\\{△>0}\\{\frac{4a+2}{8a}>2}\\{f(2)≥0}\end{array}\right.$,或$\left\{\begin{array}{l}{4a<0}\\{△>0}\\{\frac{4a+2}{8a}>2}\\{f(2)≤0}\end{array}\right.$.
即$\left\{\begin{array}{l}{4a>0}\\{(4a+2)^{2}-16a(5a+1)>0}\\{\frac{4a+2}{8a}>2}\\{13a-3≥0}\end{array}\right.$,或$\left\{\begin{array}{l}{4a<0}\\{(4a+2)^{2}-16a(5a+1)>0}\\{\frac{4a+2}{8a}>2}\\{13a-3≤0}\end{array}\right.$.
无解.
综上所述:a的取值范围是(0,$\frac{3}{13}$].
点评 本题考查了二次函数零点的个数与系数之间的关系,属于中档题.

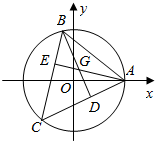 如图,点A(2,0)是一定点,定圆的方程是x2+y2=4,在定圆上取两点B、C,使得∠BAC=$\frac{π}{3}$,求△ABC的垂心G的轨迹方程.
如图,点A(2,0)是一定点,定圆的方程是x2+y2=4,在定圆上取两点B、C,使得∠BAC=$\frac{π}{3}$,求△ABC的垂心G的轨迹方程.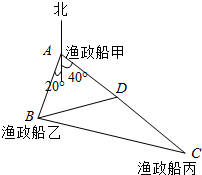 2015年6号台风“红霞”5月12日上午8点在日本本州和歌由县西南东海东部海面登陆,某渔船丙由于发动机故障急需救援,如图,正在海上A处执行任务的渔政船甲和在B处执行任务的渔政船乙,同时收到同一片海域上渔船丙的求救信号,此时渔船丙在渔政船甲的南偏东40°方向距渔政船甲140km的C处,渔政船乙在渔政船甲的南偏东西20°方向的B处,两艘渔政船协调后立即让渔政船甲向渔船丙所在位置C处沿直线AC航行前去救援,渔政船乙仍留在B处执行任务,渔政船甲航行60km到达D处时,收到新的指令另有重要任务必须执行,于是立即通知在B处执行任务的渔政船乙前去救援渔船丙(渔政船乙沿着直线BC航行前去救援渔船丙),此时B、D两处相距84km,问渔政船乙要航行多少距离才能到达渔船所在的位置C处实施营救.
2015年6号台风“红霞”5月12日上午8点在日本本州和歌由县西南东海东部海面登陆,某渔船丙由于发动机故障急需救援,如图,正在海上A处执行任务的渔政船甲和在B处执行任务的渔政船乙,同时收到同一片海域上渔船丙的求救信号,此时渔船丙在渔政船甲的南偏东40°方向距渔政船甲140km的C处,渔政船乙在渔政船甲的南偏东西20°方向的B处,两艘渔政船协调后立即让渔政船甲向渔船丙所在位置C处沿直线AC航行前去救援,渔政船乙仍留在B处执行任务,渔政船甲航行60km到达D处时,收到新的指令另有重要任务必须执行,于是立即通知在B处执行任务的渔政船乙前去救援渔船丙(渔政船乙沿着直线BC航行前去救援渔船丙),此时B、D两处相距84km,问渔政船乙要航行多少距离才能到达渔船所在的位置C处实施营救.