题目内容
(2013•通州区一模)对任意两个实数x1,x2,定义max(x1,x2)=
若f(x)=x2-2,g(x)=-x,则max(f(x),g(x))的最小值为
|
-1
-1
.分析:通过求解不等式x2-2≥-x,得出f(x)≥g(x)和f(x)<g(x)的x的取值范围,结合新定义得到分段函数
max(f(x),g(x))的解析式,在平面直角坐标系中作出分段函数的图象,则分段函数的最小值可求.
max(f(x),g(x))的解析式,在平面直角坐标系中作出分段函数的图象,则分段函数的最小值可求.
解答:解:因为对任意两个实数x1,x2,定义max(x1,x2)=
,
又f(x)=x2-2,g(x)=-x,
由x2-2≥-x,得x≤-2或x≥1,则当x2-2<-x时,得-2<x<1.
所以y=max(f(x),g(x))
,
其图象如图,
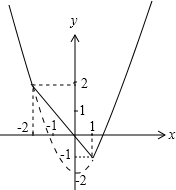
由图象可知函数max(f(x),g(x))的最小值为-1.
故答案为-1.
|
又f(x)=x2-2,g(x)=-x,
由x2-2≥-x,得x≤-2或x≥1,则当x2-2<-x时,得-2<x<1.
所以y=max(f(x),g(x))
|
其图象如图,

由图象可知函数max(f(x),g(x))的最小值为-1.
故答案为-1.
点评:本题考查了新定义,考查了函数的图象与图象的变化,考查了分段函数图象的画法,分段函数的值域要分段求,最后取并集,是基础题.

练习册系列答案
相关题目