Question

（2013•通州区一模）已知圆的直角坐标方程为x²+y²-2y=0．在以原点为极点，x轴正半轴为极轴的极坐标系中，该圆的方程为（　　）

A．ρ=2cosθ

B．ρ=2sinθ

C．ρ=-2cosθ

D．ρ=-2sinθ

Answer 1

分析：法一：利用直角坐标与极坐标间的关系，即利用ρcosθ=x，ρsinθ=y，ρ²=x²+y²，进行代换即得圆的极坐标方程
法二：设M（ρ，θ）是圆C上任一点，∠MOx=θ，利用直角三角形而出ρ，θ关系式即可．

解答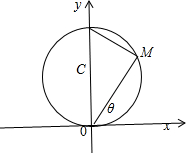：解：法一：利用直角坐标与极坐标间的关系，即利用ρcosθ=x，ρsinθ=y，ρ²=x²+y²，进行代换，
圆的直角坐标方程为x²+y²-2y=0，所以ρ²-2ρsinθ=0，即ρ=2sinθ．
法二：圆的直角坐标方程为x²+y²-2y=0，即x²+（y-1）²=1，
设M（ρ，θ）是圆C上任一点，∠MOx=θ，若θ为钝角，则sin（π-θ）=sinθ
所以2sinθ=ρ．
故选B．

点评：本题考查圆的极坐标方程求解，分别用到了定义法和转化代换法．