题目内容
(08年龙岩一中模拟)(14分)
已知函数![]()
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若![]() 存在单调递减区间,求
存在单调递减区间,求![]() 的取值范围;
的取值范围;
(Ⅲ)当![]() 时,设函数
时,设函数![]() 的图象
的图象![]() 与函数
与函数![]() 的图象
的图象![]() 交于点P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,则是否存在点R,使C1在点M处的切线与C2在点N处的切线平行?如果存在,请求出R的横坐标,如果不存在,请说明理由.
交于点P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,则是否存在点R,使C1在点M处的切线与C2在点N处的切线平行?如果存在,请求出R的横坐标,如果不存在,请说明理由.
解析:(I)解:当![]() 时,
时,![]()
则![]() ,
,
![]() 的定义域为
的定义域为![]() ,令
,令![]() =0 ,得
=0 ,得![]() ……… 2分
……… 2分
![]() 当
当![]() 时,
时,![]()
![]() ,
,![]() 在
在![]() 上是单调递增;
上是单调递增;
当![]() 时,
时,![]()
![]() ,
,![]() 在
在![]() 上是单调递减;
上是单调递减;
所以,函数![]() 的单调递增区间为
的单调递增区间为![]() ;
;
单调递减区间为![]() . ………………………… 4分
. ………………………… 4分
(II)b=2时,![]()
则![]()
因为函数![]() 存在单调递减区间,所以
存在单调递减区间,所以![]() <0有解.
<0有解.
即当x>0时,则![]() . ………………………… 5分
. ………………………… 5分
①当a=0时,![]() 为单调递增的一次函数,
为单调递增的一次函数,![]() >0在(0,+∞)总有解.
>0在(0,+∞)总有解.
②当a>0时,![]() 为开口向上的抛物线,
为开口向上的抛物线,![]() >0在(0,+∞)总有解.
>0在(0,+∞)总有解.
③当a<0时,![]() 为开口向下的抛物线,而
为开口向下的抛物线,而![]() >0在(0,+∞)总有解.
>0在(0,+∞)总有解.
则△=4+4a>0,且方程![]() =0至少有一个正根,此时,-1<a<0
=0至少有一个正根,此时,-1<a<0
综上所述,a的取值范围为(-1,+∞) ………………………… 9分
(III)证:设点P、Q的坐标是![]()
则点M、N的横坐标为![]()
C1点在M处的切线斜率为![]()
C2点N处的切线斜率为![]() ……………… 10分
……………… 10分
假设C1点M处的切线与C2在点N处的切线平行,则k1=k2
即![]() 则
则
![]()
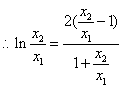 .
.
设![]() ,则
,则![]() ① ………………………… 12分
① ………………………… 12分
令![]() 则
则![]()
因为t>1时,![]() ,所以r(t)在
,所以r(t)在![]() 上单调递增.故
上单调递增.故![]()
则![]() .这与①矛盾,假设不成立.
.这与①矛盾,假设不成立.
故C1在点M处的切线与C2在点N处的切线不平行. ………………………… 14分

