题目内容
已知f′(x)是f(x)的导函数,f(x)=ln(x+1)+m-2f′(1),m∈R,且函数f(x)的图象过点(0,-2).
(1)求函数y=f(x)的表达式;
(2)设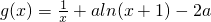 在点(1,g(1))处的切线与y轴垂直,求g(x)的极大值.
在点(1,g(1))处的切线与y轴垂直,求g(x)的极大值.
解:(1)由已知得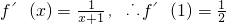 (2分)
(2分)
又f(0)=-2∴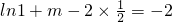 (4分)
(4分)
∴m=-1,(5分)
∴f(x)=ln(x+1)-2(6分)
(2)∵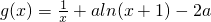 .
.
∴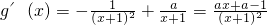 .(8分)
.(8分)
又x∈(-1,0)∪(0,+∞)
由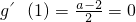 ,得a=2(10分)
,得a=2(10分)
∴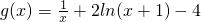
∴
由g'(x)>0,解得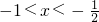 或x>1;
或x>1;
由g'(x)<0,解得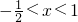 或x≠0.(12分)
或x≠0.(12分)
则g(x)的单调增区间是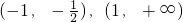 ,
,
单调递减区间是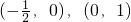 .
.
故g(x)极大值为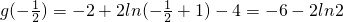 ,
,
极小值为g(1)=1+2ln2-4=-3+2ln2.(14分)
分析:(1)对函数求导可得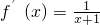 ,从而可得
,从而可得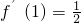 ,由函数f(x)的图象过点(0,-2)可得f(0)=-2代入可求.
,由函数f(x)的图象过点(0,-2)可得f(0)=-2代入可求.
(2)对函数g(x)求导,由题意可得g′(1)=0,代入可求a的值及函数g(x),研究函数g(x)的单调性,结合单调性求函数的极大值.
点评:本题考查了函数导数的几何意义:函数在某点的导数值即为改点的切线的斜率,属于基本知识、基本运算的考查.
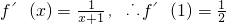 (2分)
(2分)又f(0)=-2∴
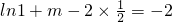 (4分)
(4分)∴m=-1,(5分)
∴f(x)=ln(x+1)-2(6分)
(2)∵
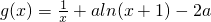 .
.∴
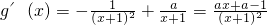 .(8分)
.(8分)又x∈(-1,0)∪(0,+∞)
由
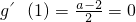 ,得a=2(10分)
,得a=2(10分)∴
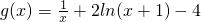
∴

由g'(x)>0,解得
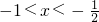 或x>1;
或x>1;由g'(x)<0,解得
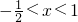 或x≠0.(12分)
或x≠0.(12分)则g(x)的单调增区间是
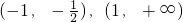 ,
,单调递减区间是
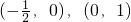 .
.故g(x)极大值为
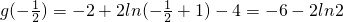 ,
,极小值为g(1)=1+2ln2-4=-3+2ln2.(14分)
分析:(1)对函数求导可得
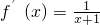 ,从而可得
,从而可得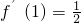 ,由函数f(x)的图象过点(0,-2)可得f(0)=-2代入可求.
,由函数f(x)的图象过点(0,-2)可得f(0)=-2代入可求.(2)对函数g(x)求导,由题意可得g′(1)=0,代入可求a的值及函数g(x),研究函数g(x)的单调性,结合单调性求函数的极大值.
点评:本题考查了函数导数的几何意义:函数在某点的导数值即为改点的切线的斜率,属于基本知识、基本运算的考查.

练习册系列答案
相关题目