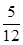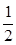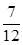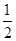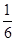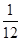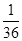题目内容
设连续掷两次骰子得到的点数分别为m、n,令平面向量a=(m,n),b=(1,-3).
(1) 求使得事件“a⊥b”发生的概率;
(2) 求使得事件“|a|≤|b|”发生的概率.
(1) 求使得事件“a⊥b”发生的概率;
(2) 求使得事件“|a|≤|b|”发生的概率.
(1) 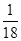 (2)
(2) 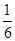
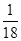 (2)
(2) 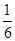
(1) 由题意知,m∈{1,2,3,4,5,6},n∈{1,2,3,4,5,6},故(m,n)所有可能的取法共36种.使得a⊥b,即m-3n=0,即m=3n,共有2种:(3,1)、(6,2),所以事件a⊥b的概率为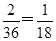 .
.
(2) |a|≤|b|,即m2+n2≤10,共有(1,1)、(1,2)、(1,3)、(2,1)、(2,2)、(3,1)6种使得|a|≤|b|,其概率为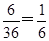
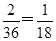 .
.(2) |a|≤|b|,即m2+n2≤10,共有(1,1)、(1,2)、(1,3)、(2,1)、(2,2)、(3,1)6种使得|a|≤|b|,其概率为
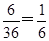

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目