题目内容
1.设函数f(x)=x|x-a|+b,a,b∈R(Ⅰ)当a>0时,讨论函数f(x)的零点个数;
(Ⅱ)若对于给定的实数a(-1<a<0),存在实数b,使不等式x-$\frac{1}{2}≤f(x)≤x+\frac{1}{2}$对于任意x∈[2a-1,2a+1]恒成立.试将最大实数b表示为关于a的函数m(a),并求m(a)的取值范围.
分析 (Ⅰ)求出函数f(x)的表达式,讨论a,b的取值即可求函数f(x)的零点个数;
(Ⅱ)根据函数恒成立,转化为求函数的最值,求出m(a)的表达式进行求解即可.
解答 解:(Ⅰ)f(x)=$\left\{\begin{array}{l}{{x}^{2}-ax+b,}&{x≥a}\\{-{x}^{2}+ax+b,}&{x<a}\end{array}\right.$,
∵a>0,
∴当b>0时,x2-ax+b=0在x≥a上无解,-x2+ax+b=0在x<a上恰有一解,
当b=0时,x2-ax+b=0在x≥a上恰有一解,-x2+ax+b=0在x<a上恰有一解,此时函数f(x)有2个零点,
当b<0时,x2-ax+b=0在x≥a上恰有一解,
若判别式△=a2+4b<0,则-x2+ax+b=0在x<a上无解,
判别式△=a2+4b=0,则-x2+ax+b=0在x<a上恰有一解,
判别式△=a2+4b>0,则-x2+ax+b=0在x<a上恰有两个不同的解,
综上在a>0的条件下,
当$\left\{\begin{array}{l}{a>0}\\{b>0}\end{array}\right.$或$\left\{\begin{array}{l}{a>0}\\{b+\frac{{a}^{2}}{4}<0}\end{array}\right.$时,函数f(x)有一个零点,
当$\left\{\begin{array}{l}{a>0}\\{b=0}\end{array}\right.$或$\left\{\begin{array}{l}{a>0}\\{b+\frac{{a}^{2}}{4}=0}\end{array}\right.$时,函数f(x)有2个零点,
当$\left\{\begin{array}{l}{a>0}\\{-\frac{{a}^{2}}{4}<b<0}\end{array}\right.$时,函数f(x)有3个零点.
(Ⅱ)首先记g(x)=f(x)-x=$\left\{\begin{array}{l}{{x}^{2}-(a+1)x+b,}&{x≥a}\\{-{x}^{2}+(a-1)x+b,}&{x<a}\end{array}\right.$,
原问题等价于:当2a-1≤x≤2a+1时,g(x)max-g(x)min≤1,
最大实数b,即g(x)max=$\frac{1}{2}$时的b的值,
令T=g(x)max-g(x)min,
由已知可得2a+1>a,2a-1<$\frac{a-1}{2}$,$\frac{a-1}{2}$<$\frac{a+1}{2}$.
(1)当-1<a<$-\frac{1}{3}$时,2a-1$<\frac{a-1}{2}<a<2a+1<\frac{a+1}{2}$,
∴g(x)在[2a-1,$\frac{a-1}{2}$]上为增函数,在[$\frac{a-1}{2}$,2a+1]上为减函数,
∴g(x)max=g($\frac{a-1}{2}$)=$\frac{(a-1)^{2}}{4}+b$,
g(x)min=min{g(2a-1),g(2a+1)}=g(2a-1)=-2a2+a+b
∴T=$\frac{(a-1)^{2}}{4}+b$-(-2a2+a+b)=$\frac{9{a}^{2}-6a+1}{4}≤1$,
解得$-\frac{1}{3}≤a≤1$,从而无解.
(2)当$-\frac{1}{3}$≤a<0时,2a-1<$\frac{a-1}{2}$<a<$\frac{a+1}{2}$<2a+1,
∴g(x)在[2a-1,$\frac{a-1}{2}$]上为增函数,在[$\frac{a-1}{2}$,$\frac{a+1}{2}$]上为减函数,在[$\frac{a+1}{2}$,2a+1]上为增函数,
∴当2a-1≤x≤2a+1,
∴g(x)max=max{g($\frac{a-1}{2}$),g(2a+1)}={g($\frac{a-1}{2}$)=$\frac{(a-1)^{2}}{4}+b$,
g(x)min=min{g(2a-1),g($\frac{a+1}{2}$)}=$\left\{\begin{array}{l}{-2{a}^{2}+a+b,}&{-\frac{1}{3}≤a≤-\frac{1}{7}}\\{b-\frac{(a+1)^{2}}{4},}&{-\frac{1}{7}<a<0}\end{array}\right.$,
∴T=$\left\{\begin{array}{l}{\frac{9{a}^{2}-6a+1}{4},}&{-\frac{1}{3}≤a≤-\frac{1}{7}}\\{\frac{{a}^{2}+1}{2},}&{-\frac{1}{7}<a<0}\end{array}\right.$,
由T≤1,解得$-\frac{1}{3}$≤a<0,
此时最大的b满足g($\frac{a-1}{2}$)=$\frac{1}{2}$,
从而bmax=m(a)=$\frac{1}{2}-\frac{(a-1)^{2}}{4}=\frac{-{a}^{2}+2a+1}{4}$,
∴m(a)=$\frac{-{a}^{2}+2a+1}{4}$,($-\frac{1}{3}$≤a<0),
解得m(a)的取值范围是[$\frac{1}{18}$,$\frac{1}{4}$)
点评 本题主要考查函数的零点的判断,以及函数恒成立问题,考查学生的分类讨论的数学思想,综合性较强,难度较大.

 一个几何体的三视图如图所示,若该几何体的各顶点都在同一个球面上,则该几何体的侧视图的面积为 ( )
一个几何体的三视图如图所示,若该几何体的各顶点都在同一个球面上,则该几何体的侧视图的面积为 ( )| A. | 4+$\sqrt{2}$ | B. | 4+$\sqrt{3}$ | C. | 3+$\sqrt{2}$ | D. | 3+$\sqrt{3}$ |
 如图,过圆外一点P作圆的两条割线,分别交圆于点A,B,C,D,PA=2,AB=4,CD=1,且圆心O恰在BC上,则该圆的半径长为$\frac{\sqrt{21}}{2}$.
如图,过圆外一点P作圆的两条割线,分别交圆于点A,B,C,D,PA=2,AB=4,CD=1,且圆心O恰在BC上,则该圆的半径长为$\frac{\sqrt{21}}{2}$. 如图,△ABC内接于直径为BC的圆O,过点A作圆O的切线交CB的延长线于点P,∠BAC的平分线分别交BC和圆O于点D、E,若sin∠ABC=$\frac{2\sqrt{5}}{5}$,PA=10.
如图,△ABC内接于直径为BC的圆O,过点A作圆O的切线交CB的延长线于点P,∠BAC的平分线分别交BC和圆O于点D、E,若sin∠ABC=$\frac{2\sqrt{5}}{5}$,PA=10.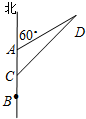 如图,机车甲、乙分别停在A,B处,且AB=10km,甲的速度为4千米/小时,乙的速度是甲的$\frac{1}{2}$,甲沿北偏东60°的方向移动,乙沿正北方向移动,若两者同时移动100分钟,则它们之间的距离为$\frac{20\sqrt{3}}{3}$千米.
如图,机车甲、乙分别停在A,B处,且AB=10km,甲的速度为4千米/小时,乙的速度是甲的$\frac{1}{2}$,甲沿北偏东60°的方向移动,乙沿正北方向移动,若两者同时移动100分钟,则它们之间的距离为$\frac{20\sqrt{3}}{3}$千米.