题目内容
已知椭圆C的方程为 (a>0),其焦点在x轴上,点Q
(a>0),其焦点在x轴上,点Q 为椭圆上一点.
为椭圆上一点.(1)求该椭圆的标准方程;
(2)设动点P(x,y)满足
 ,其中M、N是椭圆C上的点,直线OM与ON的斜率之积为
,其中M、N是椭圆C上的点,直线OM与ON的斜率之积为 ,求证:
,求证: 为定值;
为定值;(3)在(2)的条件下探究:是否存在两个定点A,B,使得|PA|+|PB|为定值?若存在,给出证明;若不存在,请说明理由.
【答案】分析:(1)把点Q坐标代入椭圆方程即可求得a2;
(2)设M(x1,y1),N(x2,y2),由直线OM与ON的斜率之积为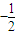 ,可得M、N坐标间的关系式,由
,可得M、N坐标间的关系式,由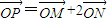 ,
,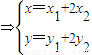 ,从而
,从而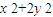 可化为M、N坐标的表达式,再由M、N是椭圆C上的点即可求得
可化为M、N坐标的表达式,再由M、N是椭圆C上的点即可求得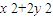 为定值;
为定值;
(3)由(2)知,动点P(x,y)满足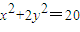 ,从而可判断点P轨迹是椭圆,其焦点即为定点A、B;
,从而可判断点P轨迹是椭圆,其焦点即为定点A、B;
解答:解:(1)因为点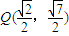 为椭圆上一点,
为椭圆上一点,
所以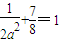 ,解得a2=4,
,解得a2=4,
所以椭圆方程为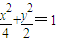 ;
;
(2)设M(x1,y1),N(x2,y2),
又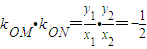 ,化简得x1x2+2y1y2=0,
,化简得x1x2+2y1y2=0,
又M、N是椭圆C上的点,所以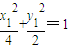 ,
,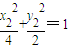 ,即
,即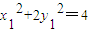 ,
,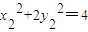 ,
,
由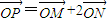 ,
,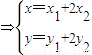 ,
,
所以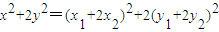
=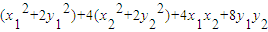
=4+4×4+4(x1x2+2y1y2)
=20(定值);
(3)由(2)知,动点P(x,y)满足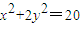 ,即
,即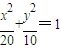 ,
,
所以点P的轨迹是以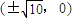 为焦点的椭圆.
为焦点的椭圆.
故存在点A(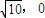 )、B(
)、B(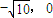 ),使得|PA|+|PB|=
),使得|PA|+|PB|=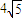 (定值).
(定值).
点评:本题考查直线与圆锥曲线的位置关系、椭圆方程的求解及平面向量基本定理,考查学生对问题的理解分析能力及解决问题的能力,具有一定综合性.
(2)设M(x1,y1),N(x2,y2),由直线OM与ON的斜率之积为
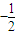 ,可得M、N坐标间的关系式,由
,可得M、N坐标间的关系式,由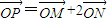 ,
,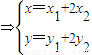 ,从而
,从而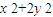 可化为M、N坐标的表达式,再由M、N是椭圆C上的点即可求得
可化为M、N坐标的表达式,再由M、N是椭圆C上的点即可求得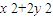 为定值;
为定值;(3)由(2)知,动点P(x,y)满足
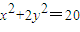 ,从而可判断点P轨迹是椭圆,其焦点即为定点A、B;
,从而可判断点P轨迹是椭圆,其焦点即为定点A、B;解答:解:(1)因为点
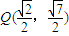 为椭圆上一点,
为椭圆上一点,所以
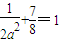 ,解得a2=4,
,解得a2=4,所以椭圆方程为
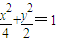 ;
;(2)设M(x1,y1),N(x2,y2),
又
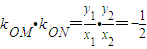 ,化简得x1x2+2y1y2=0,
,化简得x1x2+2y1y2=0,又M、N是椭圆C上的点,所以
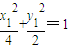 ,
,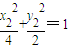 ,即
,即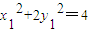 ,
,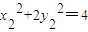 ,
,由
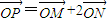 ,
,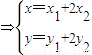 ,
,所以
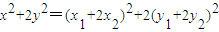
=
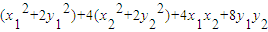
=4+4×4+4(x1x2+2y1y2)
=20(定值);
(3)由(2)知,动点P(x,y)满足
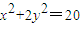 ,即
,即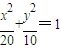 ,
,所以点P的轨迹是以
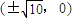 为焦点的椭圆.
为焦点的椭圆.故存在点A(
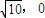 )、B(
)、B(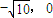 ),使得|PA|+|PB|=
),使得|PA|+|PB|=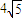 (定值).
(定值).点评:本题考查直线与圆锥曲线的位置关系、椭圆方程的求解及平面向量基本定理,考查学生对问题的理解分析能力及解决问题的能力,具有一定综合性.

练习册系列答案
相关题目