题目内容
1.用30cm的铁丝围成一个扇形,当扇形半径为$\frac{15}{2}$cm的时候扇形面积最大?分析 设出扇形的圆心角α,半径r,面积S,弧长l,根据题意求出扇形面积S的表达式,求出最大值以及对应的半径r是多少.
解答 解:设扇形的圆心角为α,半径为r,面积为S,弧长为l,
∴扇形的周长是l+2r=30;
∴l=30-2r,
∴S=$\frac{1}{2}$•l•r=$\frac{1}{2}$(30-2r)•r=-r2+15r=-(r-$\frac{15}{2}$)2+$\frac{225}{4}$
∴当半径r=$\frac{15}{2}$cm时,扇形面积的最大值是$\frac{225}{4}$cm2,
故答案为:$\frac{15}{2}$cm.
点评 本题考查了扇形面积的应用问题,解题时应建立目标函数,求目标函数的最值即可,是基础题.

练习册系列答案
相关题目
9.已知函数f(x)=ex+elnx-2ax在x∈(1,3)上单调递增,则实数a的取值范围为( )
| A. | (-∞,$\frac{{e}^{3}}{2}$+$\frac{e}{6}$) | B. | [($\frac{{e}^{3}}{2}$+$\frac{e}{6}$,+∞) | C. | (-∞,e) | D. | (-∞,e) |
6.已知单位圆与角α的终边的交点为(sin$\frac{4π}{7}$,cos$\frac{4π}{7}$),则α可能为( )
| A. | $\frac{4π}{7}$ | B. | $\frac{π}{14}$ | C. | $\frac{15π}{14}$ | D. | $\frac{27π}{14}$ |
13.函数y=xsinx的部分图象是( )
| A. |  | B. | 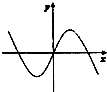 | C. | 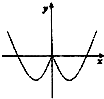 | D. |  |
 用某种型号的钢板焊接一个长为1m的无盖长方体容器(接缝忽略不计他),要求其容积为2m3,则至少需要这种型号的钢板8m2.
用某种型号的钢板焊接一个长为1m的无盖长方体容器(接缝忽略不计他),要求其容积为2m3,则至少需要这种型号的钢板8m2.