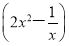Question

已知椭圆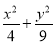＝1上任一点P，由点P向x轴作垂线PQ，垂足为Q，设点M在PQ上，且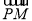＝2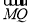，点M的轨迹为C.

(1)求曲线C的方程；

(2)过点D(0，－2)作直线l与曲线C交于A、B两点，设N是过点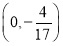且平行于x轴的直线上一动点，且满足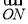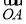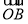＝＋ (O为原点)，且四边形OANB为矩形，求直线l的方程．

 

Answer 1

（1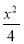）＋y2＝1（2）y＝±2x－2.

【解析】(1)设点M(x，y)是曲线C上任意一点，

∵PM⊥x轴，且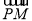＝2，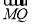

所以点P的坐标为(x,3y)，

又点P在椭圆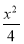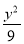＋＝1上，所以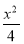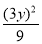＋＝1，

因此曲线C的方程是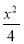＋y2＝1.

(2)当直线l的斜率不存在时，显然不满足条件，所以设直线l的方程为y＝kx－2，直线l与椭圆交于A(x1，y1)，B(x2，y2)两点．

由得(1＋4k2)x2－16kx＋12＝0，

依题意Δ＝(16k)2－48(1＋4k2)>0，得k2>(*)，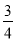

此时x1＋x2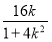＝，x1x2＝.

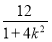因为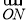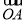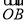＝＋，所以四边形OANB为平行四边形．

又四边形OANB是矩形，所以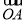·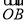＝0，

即x1x2＋y1y2＝x1x2＋k2x1x2－2k(x1＋x2)＋4＝(1＋k2)x1x2－2k(x1＋x2)＋4＝0，

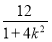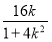∴(1＋k2)·－2k·＋4＝0，

解之得k2＝4，∴k＝±2.满足(*)式．

设N(x0，y0)，由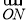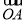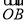＝＋，得

y0＝y1＋y2＝k(x1＋x2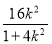)－4＝－4＝－，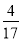

从而点N在直线y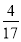＝－上，满足题设，

故直线l的方程为y＝±2x－2.