题目内容
18.已知双曲线8kx2-ky2=8的一个焦点为(0,3),则k的值为( )| A. | $\frac{{\sqrt{65}}}{3}$ | B. | $-\frac{{\sqrt{65}}}{3}$ | C. | 1 | D. | -1 |
分析 双曲线8kx2-ky2=8化为$\frac{{y}^{2}}{-\frac{8}{k}}$-$\frac{{x}^{2}}{-\frac{1}{k}}$=1,由于双曲线的一个焦点为(0,3),可得-$\frac{8}{k}$-$\frac{1}{k}$=32,解出即可
解答 解:双曲线8kx2-ky2=8
化为$\frac{{y}^{2}}{-\frac{8}{k}}$-$\frac{{x}^{2}}{-\frac{1}{k}}$=1,
∵双曲线的一个焦点为(0,3),
∴-$\frac{8}{k}$-$\frac{1}{k}$=32,
解得k=-1.
故选D.
点评 本题考查了双曲线的标准方程及其性质,考查运算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.一个口袋中有编号分别为0,1,2的小球各2个,从这6个球中任取2个,则取出2个球的编号数和的期望为( )
| A. | 1 | B. | 1.5 | C. | 2 | D. | 2.5 |
8.复数z=$\frac{1-2i}{3+4i}$(i为虚数单位)的实部为( )
| A. | -$\frac{2}{5}$ | B. | -1 | C. | -$\frac{1}{5}$ | D. | $\frac{11}{25}$ |
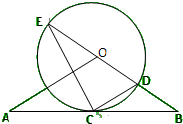 (如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,D,连接EC,CD.
(如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,D,连接EC,CD.