题目内容
在直角坐标系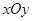 中,点
中,点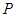 到两点
到两点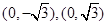 的距离之和等于4,设点
的距离之和等于4,设点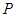 的轨迹为
的轨迹为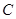 ,直线
,直线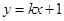 与
与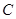 交于
交于 两点.
两点.
(1)写出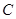 的方程;
的方程;
(2) 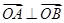 ,求
,求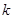 的值.
的值.
(1)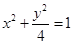 ;(2)
;(2)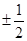 .
.
解析试题分析:(1)根据椭圆的定义,可判断点的轨迹为椭圆,再根据椭圆的基本量,容易写出椭圆的方程,求曲线的方程一般可设动点坐标为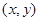 ,然后去探求动点坐标满足的方程,但如果根据特殊曲线的定义,先行判断出曲线的形状(如椭圆,圆,抛物线等),则可直接写出其方程;(2)一般地,涉及直线与二次曲线相交的问题,则可联立方程组,或解出交点坐标,或设而不求,利用一元二次方程根与系数的关系建立关系求出参数的值(取值范围),本题可设
,然后去探求动点坐标满足的方程,但如果根据特殊曲线的定义,先行判断出曲线的形状(如椭圆,圆,抛物线等),则可直接写出其方程;(2)一般地,涉及直线与二次曲线相交的问题,则可联立方程组,或解出交点坐标,或设而不求,利用一元二次方程根与系数的关系建立关系求出参数的值(取值范围),本题可设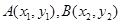 ,根据
,根据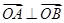 ,及
,及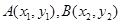 满足椭圆的方程,利用一元二次方程根与系数的关系消去坐标即得.
满足椭圆的方程,利用一元二次方程根与系数的关系消去坐标即得.
试题解析:(1)设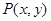 ,由椭圆定义可知,点
,由椭圆定义可知,点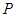 的轨迹
的轨迹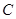 是以
是以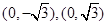 为焦点,
为焦点,
长半轴为2的椭圆, 2分
它的短半轴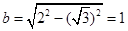 , 4分
, 4分
故曲线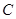 的方程为
的方程为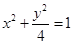 . 6分
. 6分
(2)证明:设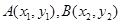 ,其坐标满足
,其坐标满足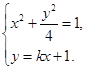 消去
消去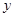 并整理,得
并整理,得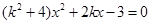 8分
8分
故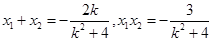 . 10分
. 10分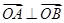 即
即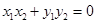 ,而
,而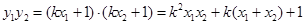 ,
,
于是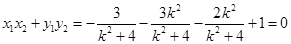 ,
,
解得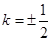 13分
13分
考点:椭圆的方程,直线与椭圆的位置关系.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案
相关题目
 的最小值.
的最小值.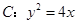 焦点为
焦点为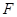 ,直线
,直线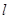 经过点
经过点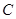 相交于
相交于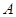 ,
,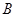 两点
两点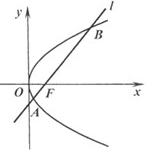
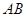 的中点在直线
的中点在直线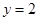 上,求直线
上,求直线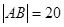 ,求直线
,求直线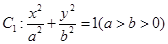 的离心率为
的离心率为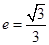 ,直线
,直线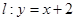 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆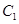 的短半轴长为半径的圆
的短半轴长为半径的圆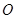 相切.
相切.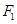 ,右焦点为
,右焦点为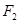 ,直线
,直线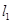 过点
过点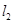 垂直于
垂直于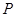 ,线段
,线段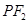 的垂直平分线交
的垂直平分线交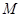 ,求点
,求点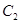 的方程;
的方程; 轴交于点
轴交于点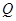 ,不同的两点
,不同的两点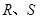 在
在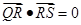 ,求
,求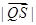 的取值范围.
的取值范围.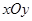 中,已知点
中,已知点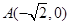 ,
,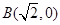 ,
,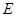 为动点,且直线
为动点,且直线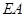 与直线
与直线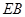 的斜率之积为
的斜率之积为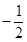 .
.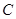 的方程;
的方程;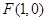 的直线
的直线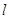 与曲线
与曲线 ,
, .若点
.若点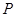 在
在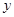 轴上,且
轴上,且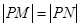 ,求点
,求点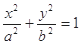 (
(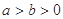 )右顶点到右焦点的距离为
)右顶点到右焦点的距离为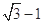 ,短轴长为
,短轴长为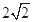 .
.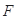 的直线与椭圆分别交于
的直线与椭圆分别交于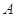 、
、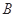 两点,若线段
两点,若线段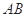 的长为
的长为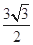 ,求直线
,求直线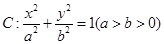 的离心率为
的离心率为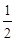 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线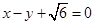 相切,直线
相切,直线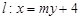 与椭圆C相交于A、B两点.
与椭圆C相交于A、B两点.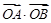 的取值范围;
的取值范围; 的左右焦点为F1,F2,离心率为
的左右焦点为F1,F2,离心率为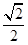 ,以线段F1 F2为直径的圆的面积为
,以线段F1 F2为直径的圆的面积为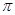 , (1)求椭圆的方程;(2) 设直线l过椭圆的右焦点F2(l不垂直坐标轴),且与椭圆交于A、B两点,线段AB的垂直平分线交x轴于点M(m,0),试求m的取值范围.
, (1)求椭圆的方程;(2) 设直线l过椭圆的右焦点F2(l不垂直坐标轴),且与椭圆交于A、B两点,线段AB的垂直平分线交x轴于点M(m,0),试求m的取值范围.
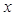 轴非负半轴,建立平面直角坐标系,且两坐标系取相同的单位长度.
轴非负半轴,建立平面直角坐标系,且两坐标系取相同的单位长度.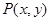 ,求
,求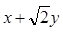 的取值范围;
的取值范围;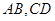 交于点
交于点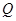 ,且直线
,且直线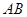 与
与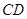 的倾斜角互补,
的倾斜角互补,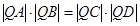 .
.