题目内容
已知O为坐标原点,| OA |
| OB |
| 3 |
| OA |
| OB |
(1)求y关于x的函数关系式f(x);
(2)若f(x)的最大值为2,求a的值;
(3)利用(2)的结论,用“五点法”作出函数f(x)在长度为一个周期的闭区间上的简图,并指出其单调区间.
分析:(1)把
和
的坐标,代入函数解析式,利用向量积的运算求得函数解析式.
(2)利用二倍角公式对函数解析式化简整理,利用正弦函数的性质表示出函数的最大值,求得a.
(3)利用(2)中的函数解析式,根据正弦函数的单调性求得函数的单调增区间和减区间.
| OA |
| OB |
(2)利用二倍角公式对函数解析式化简整理,利用正弦函数的性质表示出函数的最大值,求得a.
(3)利用(2)中的函数解析式,根据正弦函数的单调性求得函数的单调增区间和减区间.
解答: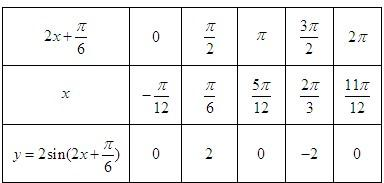 解:(1)∵
解:(1)∵
=(2cos2x,1),
=(1,
sin2x+a)
∴y=
•
=2cos2x+
sin2x+a
(2)由(1)得y=2cos2x+
sin2x+a
=1+cos2x+
sin2x+a
=cos2x+
sin2x+a+1
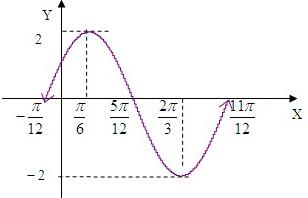 =2(
=2(
cos2x+
sin2x)+a+1
=2(sin
cos2x+cos
sin2x)+a+1
=2sin(2x+
)+a+1
当sin(2x+
)=1时,ymax=2+a+1=3+a
又∵ymax=2
∴3+a=2
∴a=-1
(3)由(2)得,y=2sin(2x+
)
增区间是:[-
+kπ,
+kπ](k∈Z),
减区间是:[
+kπ,
+kπ](k∈Z).
 解:(1)∵
解:(1)∵| OA |
| OB |
| 3 |
∴y=
| OA |
| OB |
| 3 |
(2)由(1)得y=2cos2x+
| 3 |
=1+cos2x+
| 3 |
=cos2x+
| 3 |
 =2(
=2(| 1 |
| 2 |
| ||
| 2 |
=2(sin
| π |
| 6 |
| π |
| 6 |
=2sin(2x+
| π |
| 6 |
当sin(2x+
| π |
| 6 |
又∵ymax=2
∴3+a=2
∴a=-1
(3)由(2)得,y=2sin(2x+
| π |
| 6 |
增区间是:[-
| π |
| 3 |
| π |
| 6 |
减区间是:[
| π |
| 6 |
| 2π |
| 3 |
点评:本题主要考查了三角函数的最值,二倍角的化简求值,平面向量的数量积的运算.考查了对三角函数基础知识的综合应用.

练习册系列答案
相关题目