题目内容
已知O为坐标原点,对于函数f(x)=asinx+bcosx,称向量
=(a,b)为函数f(x)的伴随向量,同时称函数f(x)为向量
的伴随函数.记
=(1,
)的伴随函数为h(x),则使得关于x的方程h(x)-t=0在[0,
]内恒有两个不相等实数解的实数t的取值范围是
| OM |
| OM |
| ON |
| 3 |
| π |
| 2 |
[
,2)
| 3 |
[
,2)
.| 3 |
分析:由题意可得,h(x)=sinx+
cosx=2sin(x+
),由 0≤x≤
,可得
≤x+
≤
.故函数y=2sinθ,θ∈[
,
],和函数 y=t有2个交点,数形结合可得t的范围.
| 3 |
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 5π |
| 6 |
| π |
| 3 |
| 5π |
| 6 |
解答: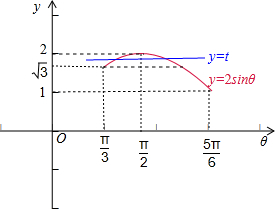 解:由题意可得,h(x)=sinx+
解:由题意可得,h(x)=sinx+
cosx=2sin(x+
),由关于x的方程h(x)-t=0在[0,
]内恒有两个不相等实数解,
可得函数h(x)的图象和直线y=t在[0,
]内恒有两个不同的交点.
由 0≤x≤
,可得
≤x+
≤
.
故函数y=2sinθ,θ∈[
,
],和函数 y=t有2个交点,故有
≤t<2,
即t的范围为[
,2),
故答案为[
,2).
 解:由题意可得,h(x)=sinx+
解:由题意可得,h(x)=sinx+| 3 |
| π |
| 3 |
| π |
| 2 |
可得函数h(x)的图象和直线y=t在[0,
| π |
| 2 |
由 0≤x≤
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 5π |
| 6 |
故函数y=2sinθ,θ∈[
| π |
| 3 |
| 5π |
| 6 |
| 3 |
即t的范围为[
| 3 |
故答案为[
| 3 |
点评:本题主要考查函数的零点和方程的根的关系,体现了转化、数形结合的数学思想,属于中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
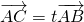 ,t∈R,令
,t∈R,令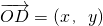 ,且
,且 与
与 的夹角为θ,则对任意t∈R,满足θ∈[0°,90°)的一个(x,y)是
的夹角为θ,则对任意t∈R,满足θ∈[0°,90°)的一个(x,y)是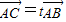 ,t∈R,令
,t∈R,令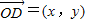 ,且
,且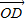 与
与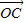 的夹角为θ,则对任意t∈R,满足θ∈[0°,90°)的一个(x,y)是( )
的夹角为θ,则对任意t∈R,满足θ∈[0°,90°)的一个(x,y)是( )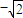 ,0)、(
,0)、(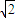 ,0),点A、N满足
,0),点A、N满足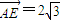 ,
,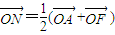 ,过点N且垂直于AF的直线交线段AE于点M,设点M的轨迹为C.
,过点N且垂直于AF的直线交线段AE于点M,设点M的轨迹为C.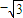 ,3k),求
,3k),求 取最大值时直线l的方程.
取最大值时直线l的方程.