题目内容
题干的形式不当若圆x2+y2-4x-4y-10=0上至少有三个不同点到直线l:ax+by=0的距离为 ,则直线l的倾斜角的取值范围是________
,则直线l的倾斜角的取值范围是________
A.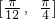 B.
B. C.
C.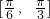 D.
D. .
.
B
分析:先求出圆心和半径,比较半径和 ;要求圆上至少有三个不同的点到直线l:ax+by=0的距离为
;要求圆上至少有三个不同的点到直线l:ax+by=0的距离为  ,则圆心到直线的距离应小于等于
,则圆心到直线的距离应小于等于  ,用圆心到直线的距离公式,可求得结果.
,用圆心到直线的距离公式,可求得结果.
解答:圆x2+y2-4x-4y-10=0整理为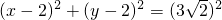 ,
,
∴圆心坐标为(2,2),半径为3 ,
,
要求圆上至少有三个不同的点到直线l:ax+by=0的距离为 ,
,
则圆心到直线的距离应小于等于 ,
,
∴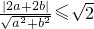 ,
,
∴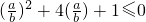 ,
,
∴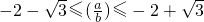 ,
, ,
,
∴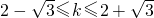 ,
,
直线l的倾斜角的取值范围是 ,
,
故选B.
点评:此题考查了直线和圆的位置关系,直线与圆相交的性质等知识,要求学生掌握点到直线的距离公式,以及直线倾斜角与斜率的关系,其中根据题意得出圆心到直线的距离应小于等于 是解本题的关键.
是解本题的关键.
分析:先求出圆心和半径,比较半径和
 ;要求圆上至少有三个不同的点到直线l:ax+by=0的距离为
;要求圆上至少有三个不同的点到直线l:ax+by=0的距离为  ,则圆心到直线的距离应小于等于
,则圆心到直线的距离应小于等于  ,用圆心到直线的距离公式,可求得结果.
,用圆心到直线的距离公式,可求得结果.解答:圆x2+y2-4x-4y-10=0整理为
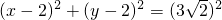 ,
,∴圆心坐标为(2,2),半径为3
 ,
,要求圆上至少有三个不同的点到直线l:ax+by=0的距离为
 ,
,则圆心到直线的距离应小于等于
 ,
,∴
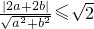 ,
,∴
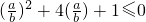 ,
,∴
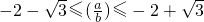 ,
, ,
,∴
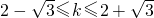 ,
,直线l的倾斜角的取值范围是
 ,
,故选B.
点评:此题考查了直线和圆的位置关系,直线与圆相交的性质等知识,要求学生掌握点到直线的距离公式,以及直线倾斜角与斜率的关系,其中根据题意得出圆心到直线的距离应小于等于
 是解本题的关键.
是解本题的关键. 
练习册系列答案
相关题目
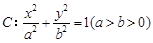 的离心率为
的离心率为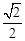 ,其中左焦点F(-2,0).
,其中左焦点F(-2,0).