题目内容
16.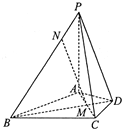 在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°,点N在线段PB上,且PN=$\sqrt{2}$.
在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°,点N在线段PB上,且PN=$\sqrt{2}$.(Ⅰ)求证:BD⊥PC;
(Ⅱ)求证:MN∥平面PDC.
分析 (Ⅰ)由正三角形的性质可得BD⊥AC,利用线面垂直的性质可知PA⊥BD,再利用线面垂直的判定定理即可证明BD⊥PC;
(Ⅱ)利用已知条件分别求出BM、MD、PB,得到$\frac{BM}{MD}=\frac{BN}{NP}$,即可得到MN∥PD,再利用线面平行的判定定理即可证明
解答 证明:(I)∵△ABC是正三角形,M是AC中点,
∴BM⊥AC,即BD⊥AC.
又∵PA⊥平面ABCD,∴PA⊥BD.
又PA∩AC=A,∴BD⊥平面PAC.
∴BD⊥PC.
(Ⅱ)在正△ABC中,BM=2$\sqrt{3}$.
在△ACD中,
∵M为AC中点,DM⊥AC,∴AD=CD.
∠ADC=120°,
∴DM=$\frac{2\sqrt{3}}{3}$,
∴$\frac{NM}{MD}$=$\frac{3}{1}$.
在等腰直角△PAB中,PA=AB=4,PB=4$\sqrt{2}$,
∴$\frac{BN}{NP}$=$\frac{3}{1}$,
∴$\frac{BM}{MD}=\frac{BN}{NP}$,
∴MN∥PD.
又MN?平面PDC,PD?平面PDC,
∴MN∥平面PDC.
点评 本题主要考查线面垂直的性质以及线面平行的判定,利用相应的判定定理和性质定理是解决本题的关键.

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
11.已知集合A={2,3},B={x|x2-4x+3=0},则A∩B等于( )
| A. | {2} | B. | {3} | C. | {1} | D. | {1,3} |
1.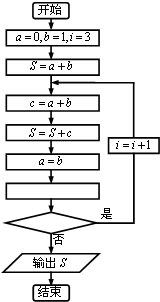 斐波那契数列是:第1项是0,第2项是1,从第三项开始,每一项都等于前两项之和.某同学设计了一个求这个数列的前10项和的程序框图,那么在空白矩形框和判断框内应分别填入的语句是( )
斐波那契数列是:第1项是0,第2项是1,从第三项开始,每一项都等于前两项之和.某同学设计了一个求这个数列的前10项和的程序框图,那么在空白矩形框和判断框内应分别填入的语句是( )
 斐波那契数列是:第1项是0,第2项是1,从第三项开始,每一项都等于前两项之和.某同学设计了一个求这个数列的前10项和的程序框图,那么在空白矩形框和判断框内应分别填入的语句是( )
斐波那契数列是:第1项是0,第2项是1,从第三项开始,每一项都等于前两项之和.某同学设计了一个求这个数列的前10项和的程序框图,那么在空白矩形框和判断框内应分别填入的语句是( )| A. | c=a,i≤9 | B. | b=c,i≤9 | C. | c=a,i≤10 | D. | b=c,i≤10 |
5.已知如图是一个空间几何体的三视图,则该几何体的体积为( )
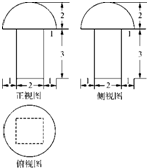

| A. | 12+$\frac{4π}{3}$ | B. | 12+$\frac{16π}{3}$ | C. | 4+$\frac{16π}{3}$ | D. | 4+$\frac{4π}{3}$ |