题目内容
【题目】已知函数![]() ,
, ![]() 为实数.
为实数.
(1)若关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,求实数
,求实数![]() 的值;
的值;
(2)设![]() ,当
,当![]() 时,求函数
时,求函数![]() 的最小值(用
的最小值(用![]() 表示);
表示);
(3)若关于![]() 不等式
不等式![]() 的解集中恰好有两个整数解,求
的解集中恰好有两个整数解,求![]() 的取值范围.
的取值范围.
【答案】(1) m=-2;(2)详见解析;(3) ![]() 或
或![]() .
.
【解析】试题分析:(1)有二次不等式的解法知,1,2是方程f(x)=0的根,进而可求实数![]() ;
;
(2)由对称轴与定义域的位置关系,结合二次图像即可得最小值;
(3)由![]() 得
得![]() ,设
,设![]() ,由
,由![]() ,所以原不等式一定有整数解x=1,故有两种情况,即{0,1}和{1,2},分别求范围即可.
,所以原不等式一定有整数解x=1,故有两种情况,即{0,1}和{1,2},分别求范围即可.
试题解析:
(1)因为不等式的解集是(1,2),所以1,2是方程f(x)=0的根,
由f(2)=0得m=-2,经验证符合题意,所以m=-2;
(2)函数![]() 的图象是开口向上的抛物线,其对称轴为
的图象是开口向上的抛物线,其对称轴为![]() ,
,
因为![]() ,所以
,所以![]() ,
,
①当![]() ,即m≥3时,函数
,即m≥3时,函数![]() 在
在![]() 单调递增,
单调递增,
则当x=-1时取得最小值![]() ;
;
②当![]() ,即
,即![]() 时,
时,
函数![]() 在
在![]() 上递减,在
上递减,在![]() 上单调递增,
上单调递增,
所以当![]() 时,函数
时,函数![]() 有最小值
有最小值![]() ;
;
综上所述,当m≥3时![]() ;当
;当![]() 时
时![]() .
.
(3)由![]() 得
得![]() ,
,
设![]() ,
,
因为![]() ,所以原不等式一定有整数解x=1.
,所以原不等式一定有整数解x=1.
因为不等式![]() 的解集中恰好有两个整数解,故有两种情况,即{0,1}和{1,2};
的解集中恰好有两个整数解,故有两种情况,即{0,1}和{1,2};
①当解集中恰好有两个整数解集为{0,1}时,有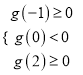 ,解得
,解得![]() ;
;
②当解集中恰好有两个整数解集为{1,2}时,有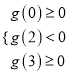 ,解得
,解得![]() ;
;
综上,m的取值范围是![]() 或
或![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】电视剧《人民的名义》中有一个低矮的接待上访服务窗口,假设群众办理业务所需的时间互相独立,且都是10分钟的整数倍,对以往群众办理业务所需的时间统计结果如下:
办理业务所需的时间(分) | 10 | 20 | 30 | 40 | 50 |
频率 | 0.3 | 0.3 | 0.2 | 0.1 | 0.1 |
假设排队等待办理业务的群众不少于3人,从第一个群众开始办理业务时开始计时.
(Ⅰ)估计第三个群众恰好等待40分钟开始办理业务的概率;
(Ⅱ)![]() 表示至第20分钟末已办理完业务的群众人数,求
表示至第20分钟末已办理完业务的群众人数,求![]() 的分布列及数学期望.
的分布列及数学期望.