题目内容
给出下列命题：
①已知直线m，l，平面α，β，若m⊥β，l?α，α∥β，则m⊥l；
②
•
＞0，是
，
的夹角为锐角的充要条件；
③若f（x）在R上满足f（x-2）=-f（x），则f（x）是以4为周期的周期函数；
④y=sin（2x+
）的图象的一个对称中心是（
，0）
以上命题正确的是
①已知直线m，l，平面α，β，若m⊥β，l?α，α∥β，则m⊥l；
②
| a |
| b |
| a |
| b |
③若f（x）在R上满足f（x-2）=-f（x），则f（x）是以4为周期的周期函数；
④y=sin（2x+
| π |
| 3 |
| π |
| 3 |
以上命题正确的是
①③④
①③④
（注：把你认为正确的命题的序号都填上）分析：已知直线m，l，平面α，β，若m⊥β，l?α，α∥β，则m⊥β，故m⊥l；当
，
同向时，
•
＞0，但
，
的夹角为0°；若f（x）在R上满足f（x-2）=-f（x），则f（x）是以4为周期的周期函数；y=sin（2x+
）的图象的一个对称中心是（
，0）．
| a |
| b |
| a |
| b |
| a |
| b |
| π |
| 3 |
| π |
| 3 |
解答：解：已知直线m，l，平面α，β，
若m⊥β，l?α，α∥β，则m⊥β，∴m⊥l．故①正确；
②当
，
同向时，
•
＞0，但
，
的夹角为0°，故②不正确；
③若f（x）在R上满足f（x-2）=-f（x），
则f（x）是以4为周期的周期函数，③正确；
④y=sin（2x+
）的图象的一个对称中心是（
，0），④正确．
故答案为：①③④．
若m⊥β，l?α，α∥β，则m⊥β，∴m⊥l．故①正确；
②当
| a |
| b |
| a |
| b |
| a |
| b |
③若f（x）在R上满足f（x-2）=-f（x），
则f（x）是以4为周期的周期函数，③正确；
④y=sin（2x+
| π |
| 3 |
| π |
| 3 |
故答案为：①③④．
点评：本题考查真假命题的判断，是基础题．解题时要注意空间两条直线的位置关系、向量的数量积、三角函数的性质等知识点的灵活运用．
练习册系列答案
相关题目
”是“|2y-x|≤2”的充分不必要条件．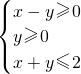
”是“|2y-x|≤2”的充分不必要条件．