题目内容
【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)设![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若![]() ,函数
,函数![]() ,试判断是否存在
,试判断是否存在![]() ,使得
,使得![]() 为函数
为函数![]() 的极小值点.
的极小值点.
【答案】(1)递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .(2)存在
.(2)存在
【解析】试题分析:(I)由题意![]() .令
.令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() .可得函数
.可得函数![]() 的单调区间.
的单调区间.
(II)由已知有![]() ,
,  .令
.令![]() ,则
,则![]() .由题可得函数
.由题可得函数![]() 在区间
在区间![]() 上单调递增.且
上单调递增.且![]() ,
, ![]() .故存在
.故存在![]()
![]() ,使得
,使得![]() ,且当
,且当![]() 时,
时, ![]() ,当
,当![]() ,
, ![]() ,所以存在
,所以存在![]() ,使得
,使得![]() 为函数
为函数![]() 的极小值点.
的极小值点.
试题解析:(I)由题意可知: ![]() ,其定义域为
,其定义域为![]() ,则
,则
![]() .
.
令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() .故函数
.故函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(II)由已知有![]() ,对于
,对于![]() ,有
,有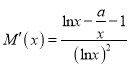 .
.
令![]() ,则
,则![]() .
.
令![]() ,有
,有![]() .
.
而![]() ,所以
,所以![]() ,故当
,故当![]() 时,
时,![]() .
.
![]() 函数
函数![]() 在区间
在区间![]() 上单调递增.
上单调递增.
注意到![]() ,
, ![]() .
.
故存在![]()
![]() ,使得
,使得![]() ,且当
,且当![]() 时,
时, ![]() ,当
,当![]() ,所以存在
,所以存在![]() ,使得
,使得![]() 为函数
为函数![]() 的极小值点.
的极小值点.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目


