题目内容
 如图△ABC,D是△ABC内一点,延长BA至点E,延长DC至点F,使得AE=CF,G,H,M分别为BD,AC,EF的中点,如果G,H,M三点共线.
如图△ABC,D是△ABC内一点,延长BA至点E,延长DC至点F,使得AE=CF,G,H,M分别为BD,AC,EF的中点,如果G,H,M三点共线.
求证:AB=CD.
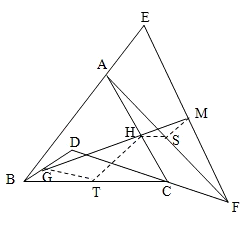 证明:
证明:取BC中点T,AF的中点S,连GT,HT,HS,SM.…(2分)
∵G,H,M分别为BD,AC,EF的中点
∴MS∥AE,
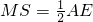 ,HS∥CF,
,HS∥CF,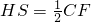 ,∵AE=CF∴HS=SM,
,∵AE=CF∴HS=SM,∴∠SHM=∠SMH…(6分)
∵GT∥CD,HT∥AB,
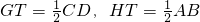
∴GT∥HS,HT∥SM…(9分)
∴∠SHM=∠TGH,∠SMH=∠THG
∴∠TGH=∠THG
∴GT=TH
∴AB=CD…(12分)
分析:由三角形的中位线得,MS∥AE,MS=
 AE,HS∥CF,HS=
AE,HS∥CF,HS= CF,由已知得HS=SM,从而得出∠SHM=∠SMH,则得出∠TGH=∠THG,GT=TH,最后不难看出AB=CD.
CF,由已知得HS=SM,从而得出∠SHM=∠SMH,则得出∠TGH=∠THG,GT=TH,最后不难看出AB=CD.点评:本题考查了三角形的中位线定理以及平行线的性质.

练习册系列答案
相关题目
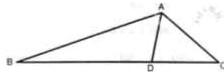 如图△ABC,D是∠BAC的平分线
如图△ABC,D是∠BAC的平分线 如图△ABC,D是△ABC内一点,延长BA至点E,延长DC至点F,使得AE=CF,G,H,M分别为BD,AC,EF的中点,如果G,H,M三点共线.
如图△ABC,D是△ABC内一点,延长BA至点E,延长DC至点F,使得AE=CF,G,H,M分别为BD,AC,EF的中点,如果G,H,M三点共线.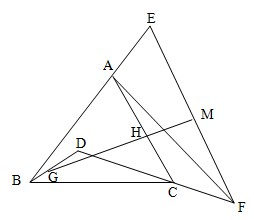
 =
= ;
;