题目内容
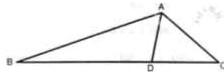如图△ABC，D是∠BAC的平分线（Ⅰ）用正弦定理证明：
| AB |
| AC |
| BD |
| DC |
（Ⅱ）若∠BAC=120°，AB=2，AC=1，求AD的长．
分析：（Ⅰ）设∠ADB=α，∠BAD=β则在△ABD中根据正弦定理
=
，同时在△ACD中根据正弦定理
=
由根据∠BAD=∠DAC，∠DCA=180°-α，进而得出
=
，进而证明
=
（Ⅱ）先由余弦定理在△ABC求出BC，再根据AB=2，AC=1，
=
求出BD和DC，在△ABD中由余弦定理得求出AD
| AB |
| BD |
| sinα |
| sinβ |
| AC |
| DC |
| sin∠ADC |
| sin∠DCA |
| sin∠ADC |
| BD∠DCA |
| sinα |
| sinβ |
| AB |
| AC |
| BD |
| DC |
（Ⅱ）先由余弦定理在△ABC求出BC，再根据AB=2，AC=1，
| AB |
| AC |
| BD |
| DC |
解答：（Ⅰ）证明：设∠ADB=α，∠BAD=β，则∠ADC=180°-α，∠CAD=β
由正弦定理得，在△ABD中，
=
①
在△ACD中，
=
，②
又sinα=sin（180°-α）③
由①②③得：
=
．
（Ⅱ）解：在△ABC中，由余弦定理得
BC2=AB2+AC2-2AB•ACcos∠BAC
=4+1-2×2×1×cos120°=7.20090209
故BC=
设BD=x，DC=y，则
x+y=
④
由（Ⅰ）得
=2，即x=2y⑤
联立④⑤解得x=
，y=
故cosB=
=
在△ABD中，由余弦定理得
AD2=AB2+BD2=2AB•BDcos∠ABD
=4+（
）2-2×2×
×
=
所以AD=
．
由正弦定理得，在△ABD中，
| AB |
| sinα |
| BD |
| sinβ |
在△ACD中，
| AC |
| sin(180°-α) |
| DC |
| sinβ |
又sinα=sin（180°-α）③
由①②③得：
| AB |
| AC |
| BD |
| DC |
（Ⅱ）解：在△ABC中，由余弦定理得
BC2=AB2+AC2-2AB•ACcos∠BAC
=4+1-2×2×1×cos120°=7.20090209
故BC=
| 7 |
设BD=x，DC=y，则
x+y=
| 7 |
由（Ⅰ）得
| x |
| y |
联立④⑤解得x=
2
| ||
| 3 |
| ||
| 3 |
故cosB=
| AB2+BC2-AC2 |
| 2AB•BC |
| 5 | ||
2
|
在△ABD中，由余弦定理得
AD2=AB2+BD2=2AB•BDcos∠ABD
=4+（
2
| ||
| 3 |
2
| ||
| 3 |
| 5 | ||
2
|
=
| 4 |
| 9 |
所以AD=
| 2 |
| 3 |
点评：本题主要考查了正弦定理和余弦定理的应用．在解三角形问题的时候往往通过这两个定理进行角和边的互化，故应灵活运用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图△ABC，D是△ABC内一点，延长BA至点E，延长DC至点F，使得AE=CF，G，H，M分别为BD，AC，EF的中点，如果G，H，M三点共线．
如图△ABC，D是△ABC内一点，延长BA至点E，延长DC至点F，使得AE=CF，G，H，M分别为BD，AC，EF的中点，如果G，H，M三点共线．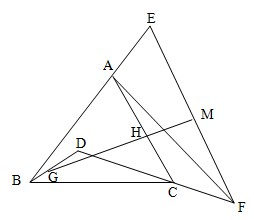
=
；