题目内容
15.双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{3}$=1的焦点到渐近线的距离为$\sqrt{3}$.分析 先由题中条件求出焦点坐标和渐近线方程,再代入点到直线的距离公式即可求出结论.
解答 解:由题得:其焦点坐标为(-$\sqrt{7}$,0),($\sqrt{7}$,0).渐近线方程为y=±$\frac{\sqrt{3}}{2}$x,即$±\sqrt{3}$x-2y=0,
所以焦点到其渐近线的距离d=$\frac{\sqrt{21}}{\sqrt{3+4}}$=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题以双曲线方程为载体,考查双曲线的标准方程,考查双曲线的几何性质,属于基础题.

练习册系列答案
相关题目
8.执行如图的程序框图,则输出S的值为( )


| A. | 2016 | B. | 2 | C. | $\frac{1}{2}$ | D. | -1 |
11.已知直线l1:ax+2y+1=0,l2:(3-a)x-y+a=0,则条件“a=1”是“l1⊥l2“的( )
| A. | 充分必要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不必要也不充分条件 |
4.某校开设A类选修课2门,B类选修课3门,一位同学从中选3门.若要求两类课程中各至少选一门,则不同的选法共有( )
| A. | 3种 | B. | 6种 | C. | 9种 | D. | 18种 |
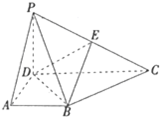 在四棱锥PABCD中,侧面PCD⊥底面ABCD,PD⊥CD,AB∥CD,∠ADC=90°,AB=AD=PD=2,CD=4
在四棱锥PABCD中,侧面PCD⊥底面ABCD,PD⊥CD,AB∥CD,∠ADC=90°,AB=AD=PD=2,CD=4 某班有60人,在三月份的月考中该班数学成绩统计得到如下频率分布直方图(满分150分,90分为及格,120分以上为优秀,且最低分数是75分).如图设第一个小矩形的高为h,各小矩形的高如图所示:
某班有60人,在三月份的月考中该班数学成绩统计得到如下频率分布直方图(满分150分,90分为及格,120分以上为优秀,且最低分数是75分).如图设第一个小矩形的高为h,各小矩形的高如图所示: