题目内容
4.设函数f(x)=min$\left\{{2\sqrt{x},|x-2|}\right\}$其中min$\{a,b\}=\left\{\begin{array}{l}a,a≤b\\ b,b≤a\end{array}$,若动直线y=m与函数y=f(x)的图象有三个交点,它们的横坐标分别为x1,x2,x3,则x1+x2+x3的范围为(4,8-2$\sqrt{3}$).分析 由f(x)表达式作出函数f(x)的图象,由图象可求得符合条件的m的取值范围,不妨设0<x1<x2<2<x3,通过解方程可用m把x1,x2,x3分别表示出来,即可求出得x1+x2+x3的取值范围
解答 解:作出函数f(x)的图象如下图所示: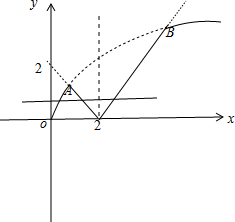 由$\left\{\begin{array}{l}{y=2\sqrt{x}}\\{y=|x-2|}\end{array}\right.$,解得A(4-2$\sqrt{3}$,2$\sqrt{3}$-2),
由$\left\{\begin{array}{l}{y=2\sqrt{x}}\\{y=|x-2|}\end{array}\right.$,解得A(4-2$\sqrt{3}$,2$\sqrt{3}$-2),
由图象可得,当直线y=m与f(x)图象有三个交点时m的范围为:0<m<2$\sqrt{3}$-2.
不妨设0<x1<x2<2<x3,
则由2$\sqrt{{x}_{1}}$=m得x1=$\frac{{m}^{2}}{4}$,由|x2-2|=2-x2=m,
得x2=2-m,由|x3-2|=x3-2=m,
得x3=m+2,且2-m>0,m+2>0,
∴x1+x2+x3=$\frac{{m}^{2}}{4}$+(2-m)+(2+m)=$\frac{{m}^{2}}{4}$+4,
当m=0时,$\frac{{m}^{2}}{4}$+4有最小值为4,
当m=2$\sqrt{3}$-2时,$\frac{{m}^{2}}{4}$+4有最大8-2$\sqrt{3}$,
∴x1+x2+x3的取值范围是(4,8-2$\sqrt{3}$)
故答案为:(4,8-2$\sqrt{3}$).
点评 本题考查函数与方程的综合运用,以及数形结合思想,综合运用知识分析解决新问题的能力,属于中档题.

练习册系列答案
相关题目
19.已知a=log42,b=log63,c=lg5,则( )
| A. | a<b<c | B. | c<a<b | C. | c<b<a | D. | b<c<a |
9.已知O为坐标原点,向量$\overrightarrow{OA}=(1,0),\overrightarrow{OB}$=(-1,2).若平面区域D由所有满足$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}$(-2≤λ≤2,-1≤μ≤1)的点C组成,则能够把区域D的周长和面积同时分为相等的两部分的曲线是( )
| A. | $y=1n\frac{5-x}{5+x}$ | B. | $y=\frac{1}{x}$ | C. | y=ex+e-x-1 | D. | y=x+cosx |
 中,
中, ,
,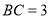 ,
, ,
, 是
是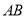 上的点,则
上的点,则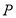 到
到 的距离的乘积的最大值为( )
的距离的乘积的最大值为( ) D.9
D.9