题目内容
(本小题满分12分)
甲、乙两人各进行3次射击,甲每次击中目标的概率为 ,乙每次击中目标的概率
,乙每次击中目标的概率 .
.
(1)记甲击中目标的次数为ξ,求ξ的概率分布列及数学期望Eξ;
(2)求甲恰好比乙多击中目标2次的概率.
甲、乙两人各进行3次射击,甲每次击中目标的概率为
 ,乙每次击中目标的概率
,乙每次击中目标的概率 .
.(1)记甲击中目标的次数为ξ,求ξ的概率分布列及数学期望Eξ;
(2)求甲恰好比乙多击中目标2次的概率.
(1)分布列(见解析),Eξ=1.5;(2) .
.
 .
.试题分析:(1)因甲每次是否击中目标相互独立,所以ξ服从二项分布,即
 ,由期望
,由期望 或
或 (二项分布);(2)甲恰好比乙多击中目标2次:分为2类,甲3次乙1次,甲2次乙0次.甲乙相互独立概率相乘.
(二项分布);(2)甲恰好比乙多击中目标2次:分为2类,甲3次乙1次,甲2次乙0次.甲乙相互独立概率相乘.试题解析:
甲射击三次其集中次数ξ服从二项分布:
(1)P(ξ=0)=
 P(ξ=1)=
P(ξ=1)=
P(ξ=2)=
 P(ξ=3)=
P(ξ=3)= 4分
4分| ξ | 0 | 1 | 2 | 3 |
| P |  |  |  |  |
Eξ=
 , 8分
, 8分(2)甲恰好比乙多击中目标2次:分为2类,甲3次乙1次,甲2次乙0次.甲乙相互独立概率相乘.
 . 12分
. 12分
练习册系列答案
相关题目

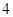 名男生和
名男生和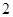 名女生中任选
名女生中任选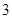 人参加演讲比赛,
人参加演讲比赛,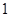 名女生的概率;
名女生的概率;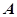 的概率是频率的稳定值,频率是概率的近似值;②一次试验中不同的基本事件不可能同时发生;③任意事件
的概率是频率的稳定值,频率是概率的近似值;②一次试验中不同的基本事件不可能同时发生;③任意事件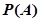 总满足
总满足 ;其中正确的是 ;(写出所有正确说法的序号)
;其中正确的是 ;(写出所有正确说法的序号)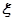 的概率分布规律为
的概率分布规律为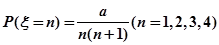 ,其中
,其中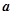 是常数,则
是常数,则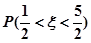 的值为( )
的值为( )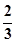
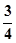
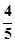
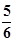
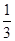 ,乙、丙去北京旅游的概率分别为
,乙、丙去北京旅游的概率分别为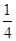 、
、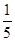 .假定三人的行动相互之间没有影响,那么这段时间内至少有一人去北京旅游的概率________.
.假定三人的行动相互之间没有影响,那么这段时间内至少有一人去北京旅游的概率________.