题目内容
(本小题满分13分)
已知椭圆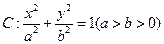 的短轴长为
的短轴长为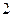 ,且与抛物线
,且与抛物线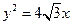 有共同的焦点,椭圆
有共同的焦点,椭圆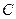 的左顶点为A,右顶点为
的左顶点为A,右顶点为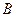 ,点
,点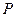 是椭圆
是椭圆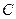 上位于
上位于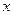 轴上方的动点,直线
轴上方的动点,直线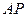 ,
,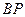 与直线
与直线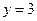 分别交于
分别交于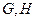 两点.
两点.
(I)求椭圆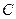 的方程;
的方程;
(Ⅱ)求线段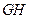 的长度的最小值;
的长度的最小值;
(Ⅲ)在线段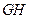 的长度取得最小值时,椭圆
的长度取得最小值时,椭圆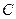 上是否存在一点
上是否存在一点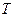 ,使得
,使得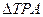 的面积为
的面积为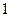 ,若存在求出点
,若存在求出点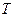 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
已知椭圆
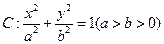 的短轴长为
的短轴长为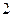 ,且与抛物线
,且与抛物线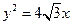 有共同的焦点,椭圆
有共同的焦点,椭圆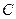 的左顶点为A,右顶点为
的左顶点为A,右顶点为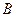 ,点
,点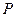 是椭圆
是椭圆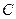 上位于
上位于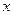 轴上方的动点,直线
轴上方的动点,直线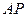 ,
,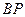 与直线
与直线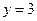 分别交于
分别交于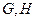 两点.
两点.(I)求椭圆
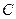 的方程;
的方程;(Ⅱ)求线段
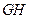 的长度的最小值;
的长度的最小值;(Ⅲ)在线段
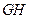 的长度取得最小值时,椭圆
的长度取得最小值时,椭圆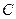 上是否存在一点
上是否存在一点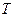 ,使得
,使得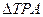 的面积为
的面积为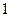 ,若存在求出点
,若存在求出点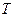 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.(1)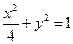 (2)8(3)
(2)8(3)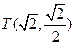 或
或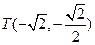
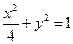 (2)8(3)
(2)8(3)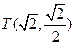 或
或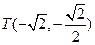
(I)由已知得,抛物线的焦点为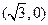 ,则
,则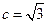 ,又
,又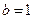 .
.
由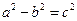 ,可得
,可得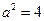 .
.
故椭圆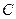 的方程为
的方程为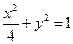 .…………………………………………4分
.…………………………………………4分
(Ⅱ)直线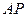 的斜率
的斜率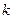 显然存在,且
显然存在,且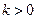 ,故可设直线
,故可设直线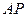 的方程为
的方程为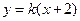 ,从而
,从而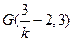 .
.
由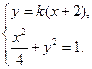 得
得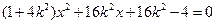 .………………………………6分
.………………………………6分
设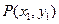 ,则
,则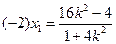 .所以
.所以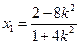 ,从而
,从而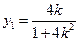 .
.
即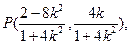 又
又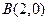 ,
,
则直线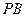 的斜率为
的斜率为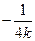 .
.
由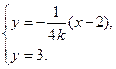 得
得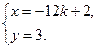
所以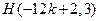 .
.
故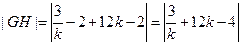 .
.
又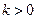 ,
,
 .
.
当且仅当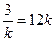 ,即
,即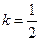 时等号成立.
时等号成立.
所以当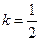 时,线段
时,线段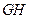 的长度取最小值
的长度取最小值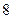 .…………………………………………8分
.…………………………………………8分
(Ⅲ)由(Ⅱ)可知,当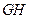 的长度取最小值时,
的长度取最小值时,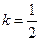 .
.
则直线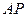 的方程为
的方程为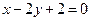 ,此时
,此时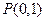 ,
,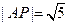 .
.
若椭圆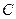 上存在点
上存在点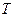 ,使得
,使得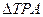 的面积等于
的面积等于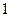 ,则点
,则点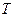 到直线
到直线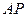 的距离等于
的距离等于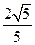 ,
,
所以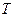 在平行于
在平行于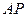 且与
且与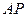 距离等于
距离等于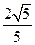 的直线
的直线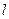 上.
上.
设直线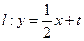 .
.
则由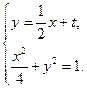 得
得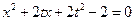 .………………………………………10分
.………………………………………10分
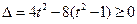 .即
.即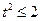 .
.
由平行线间的距离公式,得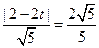 ,
,
解得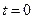 或
或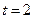 (舍去).
(舍去).
可求得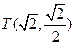 或
或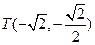 .…………………………………………13分
.…………………………………………13分
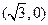 ,则
,则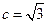 ,又
,又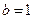 .
.由
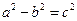 ,可得
,可得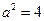 .
.故椭圆
 的方程为
的方程为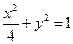 .…………………………………………4分
.…………………………………………4分(Ⅱ)直线
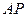 的斜率
的斜率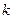 显然存在,且
显然存在,且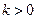 ,故可设直线
,故可设直线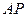 的方程为
的方程为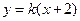 ,从而
,从而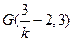 .
.由
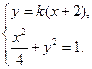 得
得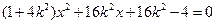 .………………………………6分
.………………………………6分设
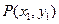 ,则
,则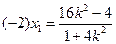 .所以
.所以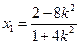 ,从而
,从而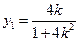 .
.即
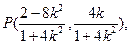 又
又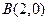 ,
,则直线
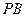 的斜率为
的斜率为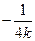 .
.由
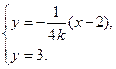 得
得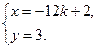
所以
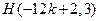 .
.故
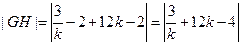 .
.又
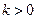 ,
,
 .
.当且仅当
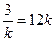 ,即
,即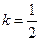 时等号成立.
时等号成立.所以当
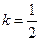 时,线段
时,线段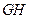 的长度取最小值
的长度取最小值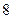 .…………………………………………8分
.…………………………………………8分(Ⅲ)由(Ⅱ)可知,当
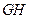 的长度取最小值时,
的长度取最小值时,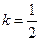 .
.则直线
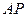 的方程为
的方程为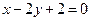 ,此时
,此时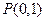 ,
,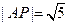 .
.若椭圆
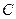 上存在点
上存在点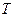 ,使得
,使得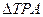 的面积等于
的面积等于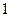 ,则点
,则点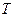 到直线
到直线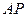 的距离等于
的距离等于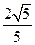 ,
,所以
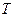 在平行于
在平行于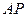 且与
且与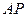 距离等于
距离等于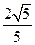 的直线
的直线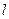 上.
上.设直线
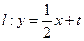 .
.则由
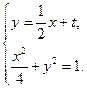 得
得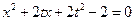 .………………………………………10分
.………………………………………10分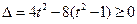 .即
.即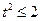 .
.由平行线间的距离公式,得
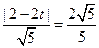 ,
,解得
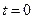 或
或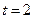 (舍去).
(舍去).可求得
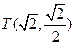 或
或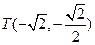 .…………………………………………13分
.…………………………………………13分
练习册系列答案
相关题目
 :
: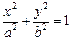 (
(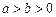 ),其左、右焦点分别为
),其左、右焦点分别为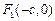 、
、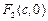 ,且
,且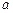 、
、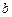 、
、 成等比数列.
成等比数列.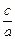 的值.
的值.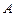 、
、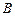 ,求证:
,求证: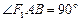 .
.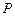 为椭圆
为椭圆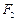 、
、 ,使
,使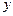 轴的交点
轴的交点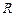 满足
满足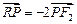 ?若存在,求直线
?若存在,求直线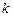 ;若不存在,请说明理由.
;若不存在,请说明理由.
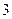 的线段
的线段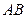 的端点
的端点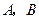 在抛物线
在抛物线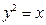 上移动,求
上移动,求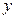 轴距离的最小值,并求出此时
轴距离的最小值,并求出此时 交于A、B两点,过原点与线段AB中点连线的斜率为
交于A、B两点,过原点与线段AB中点连线的斜率为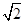 ,则
,则 的值等于( )
的值等于( ) 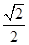 C.
C. D.
D.
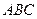 的重心
的重心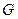 任作一直线分别交
任作一直线分别交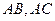 于
于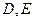 ,
,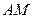 为中线
为中线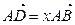 ,
,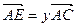 ,
,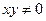 ,求
,求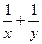 的值
的值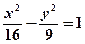 上到定点
上到定点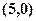 的距离是
的距离是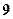 的点的个数是( )
的点的个数是( ) 个
个 个
个 个
个 个
个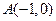 、
、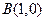 两定点,且以圆
两定点,且以圆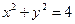 的任一条切线
的任一条切线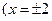 除外)为准线,则该抛物线的焦点F的轨迹方程为: ;
除外)为准线,则该抛物线的焦点F的轨迹方程为: ;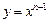 (
(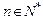 )在点
)在点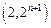 处的切线与
处的切线与 轴交点的横坐标为
轴交点的横坐标为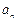 ,则
,则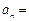 .
.