题目内容
11.已知数列{an}是等差数列,bn=${a}_{n+1}^{2}$-${a}_{n}^{2}$(n∈N+).(1)求证:数列{bn}是等差数列;
(2)若数列{an}的公差为8,b1=16,求数列{an}的前n项和Sn.
分析 (1)设等差数列{an}的公差是d,根据等差数列的通项公式化简bn+1-bn,由等差数列的定义可证明数列{bn}是等差数列;
(2)由题意和等差数列的通项公式求出a1,由等差数列的前n项公式求出数列{an}的前n项和Sn.
解答 证明:(1)设等差数列{an}的公差是d,
∵bn=${a}_{n+1}^{2}$-${a}_{n}^{2}$(n∈N+),
∴bn+1-bn=${a}_{n+2}^{2}$-${a}_{n+1}^{2}$-(${a}_{n+1}^{2}$-${a}_{n}^{2}$)
=(an+2-an+1)(an+2+an+1)-(an+1-an)(an+1+an)
=d[(an+2+an+1)-(an+1+an)]=2d2(常数),
∴数列{bn}是以2d2等差数列;
解:(2)∵数列{an}的公差为8,b1=16,
∴b1=${a}_{2}^{2}$-${a}_{1}^{2}$=16,则8(a2+a1)=16,
解得a1=-3,
∴数列{an}的前n项和Sn=na1+$\frac{n(n-1)}{2}×d$
=-3n+4n(n-1)=4n2-7n.
点评 本题考查等差数列的定义、通项公式、前n项公式的应用,以及等差数列的证明,属于中档题.

练习册系列答案
相关题目
19.若定义在R上的奇函数f(x)在(-∞,0)上是减函数,且x1+x2>0,x2+x3>0,x3+x1>0,f(x1)+f(x2)+f(x3)的值( )
| A. | 大于0 | B. | 小于0 | C. | 等于0 | D. | 大于或等于0 |
6.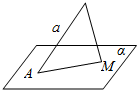 已知AB是面α的斜线段,斜足为A,AB=a,点M是面α内的动点,△ABM的面积为定值b,则点M的轨迹是( )
已知AB是面α的斜线段,斜足为A,AB=a,点M是面α内的动点,△ABM的面积为定值b,则点M的轨迹是( )
 已知AB是面α的斜线段,斜足为A,AB=a,点M是面α内的动点,△ABM的面积为定值b,则点M的轨迹是( )
已知AB是面α的斜线段,斜足为A,AB=a,点M是面α内的动点,△ABM的面积为定值b,则点M的轨迹是( )| A. | 线段 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
18.已知函数y=f(x)的图象如图,那么f(x)的表达式为( )
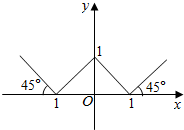

| A. | $\sqrt{{x}^{2}-2x+1}$ | B. | $\sqrt{{x}^{2}-2|x|+1}$ | C. | |x2-1| | D. | -2|x|+1 |