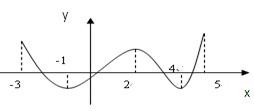
题目内容
函数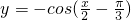 的单调递增区间是
的单调递增区间是
- A.
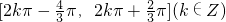
- B.
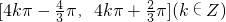
- C.
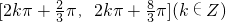
- D.
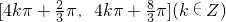
D
分析:由关于x轴的对称性可知,函数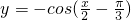 的增区间为函数
的增区间为函数 的减区间,根据余弦函数的单调递减区间列出关于x的不等式,求出不等式的解集即可得到所求函数的递增区间.
的减区间,根据余弦函数的单调递减区间列出关于x的不等式,求出不等式的解集即可得到所求函数的递增区间.
解答:由题意可知, 的单调递减区间为[2kπ,2kπ+π](k∈Z),
的单调递减区间为[2kπ,2kπ+π](k∈Z),
即2kπ≤ -
- ≤2kπ+π,
≤2kπ+π,
解得:4kπ+ π≤x≤4kπ+
π≤x≤4kπ+ π,
π,
则函数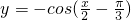 的单调递增区间是
的单调递增区间是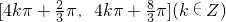 .
.
故选D
点评:此题考查了余弦函数的单调性,以及关于x轴对称的两函数之间的关系.理解函数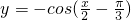 的增区间为函数
的增区间为函数 的减区间是解本题的突破点.
的减区间是解本题的突破点.
分析:由关于x轴的对称性可知,函数
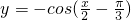 的增区间为函数
的增区间为函数 的减区间,根据余弦函数的单调递减区间列出关于x的不等式,求出不等式的解集即可得到所求函数的递增区间.
的减区间,根据余弦函数的单调递减区间列出关于x的不等式,求出不等式的解集即可得到所求函数的递增区间.解答:由题意可知,
 的单调递减区间为[2kπ,2kπ+π](k∈Z),
的单调递减区间为[2kπ,2kπ+π](k∈Z),即2kπ≤
 -
- ≤2kπ+π,
≤2kπ+π,解得:4kπ+
 π≤x≤4kπ+
π≤x≤4kπ+ π,
π,则函数
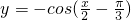 的单调递增区间是
的单调递增区间是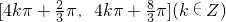 .
.故选D
点评:此题考查了余弦函数的单调性,以及关于x轴对称的两函数之间的关系.理解函数
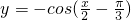 的增区间为函数
的增区间为函数 的减区间是解本题的突破点.
的减区间是解本题的突破点. 
练习册系列答案
相关题目