题目内容
动点A(x,y)在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周.已知时间t=0时,点A的坐标是(
| ||
| 2 |
| 1 |
| 2 |
分析:点A的初始角为60°,当点A转过的角度在[0°,30°]或[210°,360°]时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增,再把角度区间转化为对应的时间区间.
解答:解:t=0时,点A的坐标是 (
,
),
∴点A的初始角为30°,
当点A转过的角度在[0°,60°]或[240°,360°]时,
动点A的纵坐标y关于t(单位:秒)的函数的单调递增,
∵12秒旋转一周,
∴每秒转过的角度是360°÷12=30°,240°÷30=8,
则当0≤t≤12时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区间是[0,2],[8,12]
故答案为:[0,2],[8,12]或(0,2),(8,12).
| ||
| 2 |
| 1 |
| 2 |
∴点A的初始角为30°,
当点A转过的角度在[0°,60°]或[240°,360°]时,
动点A的纵坐标y关于t(单位:秒)的函数的单调递增,
∵12秒旋转一周,
∴每秒转过的角度是360°÷12=30°,240°÷30=8,
则当0≤t≤12时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区间是[0,2],[8,12]
故答案为:[0,2],[8,12]或(0,2),(8,12).
点评:本题考查函数的单调性及单调区间,体现了转化的数学思想.

练习册系列答案
相关题目
动点A(x,y)在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周.已知时间t=0时,点A的坐标是(
,
),则当0≤t≤12时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区间是( )
| 1 |
| 2 |
| ||
| 2 |
| A、[0,1] |
| B、[1,7] |
| C、[7,12] |
| D、[0,1]和[7,12] |
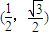 ,则当0≤t≤12时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区间是( )
,则当0≤t≤12时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区间是( )