题目内容
设函数
，（
）
（I）求函数
的最小正周期和单调递增区间；
（Ⅱ）当
时，求的最大值．
解: （I）的最小正周期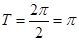
．
函数的单调递增区间是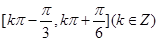 
．
（Ⅱ）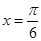
,的最大值是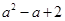
．
解析
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
天天向上一本好卷系列答案小学生10分钟应用题系列答案题目内容
设函数，（）
（I）求函数的最小正周期和单调递增区间；
（Ⅱ）当时，求的最大值．
解: （I）的最小正周期．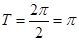
函数的单调递增区间是 ．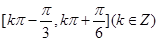
（Ⅱ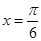）,的最大值是．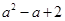
解析
天天向上一本好卷系列答案小学生10分钟应用题系列答案
。
的振幅和最小正周期；
时,函数
时，求
化成
的形式；
的值；
，
，设函数
的图象关于直线
对称，其中
，
为常数，且
. 
的最小正周期；
的图象经过点
，求函数
上的取值范围.
，
，
，
．
的最小正周期和对称中心；
上的单调递增区间．
，
，设函数
的图象关于直线
对称，其中
，
为常数，且
. 
的最小正周期； 
的图象经过点
，求函数
上的取值范围. 
是函数
图象的一条对称轴．
的值；
在
上的图象简图（不要求书写作图过程）． 
，
.
的最小正周期；（2）求
，求
的值. 
，求
时函数
的最值。